Лекция 6

Тема: Классификация плоских механизмов по Ассуру. Способы образования механизмов. Структурная классификация плоских механизмов.

План лекции.

Классификация плоских механизмов по Ассуру

Начиная с конца XVIII века учёными предлагались различные системы классификаций, основанные на делении механизмов по различным признакам: 1) по характеру движения звеньев; 2) по признаку преобразования скоростей; 3) по целевому назначению и так далее. Но ни одна из этих классификаций не обеспечивала полного охвата всех существующих механизмов. В 1914 году профессор Петербургского политехнического института Ассур предложил классификацию механизмов, которая оказалась наиболее рациональной и значительно повлияла на развитие теории механизмов и машин. Классификации Ассура подчиняются плоские механизмы, в состав которых входят только низшие кинематические пары.

Рациональность классификации Ассура заключается в том, что она: 1) указывает пути образования механизмов; 2) увязывается с методами кинематического и кинетостатического исследования механизмов, то есть каждой группе механизмов в классификации Ассура соответствуют определённые методы исследования.

Группа механизма (кинематическая цепь), у которой степень подвижности равна степени подвижности всего механизма, называется группой начальных звеньев. Кинематические цепи, у которых степень подвижности равна нулю, называется группами Ассура. Следовательно, любой механизм можно представить состоящим из одной группы начальных звеньев и одной или нескольких групп Ассура.

Группа начальных звеньев

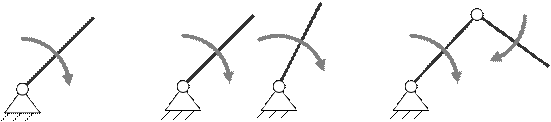
В состав этой группы обязательно входит неподвижное звено (стойка) и одно или несколько звеньев, образующих с неподвижным звеном, а иногда и друг с другом, кинематические пары 5 – го класса (по условию вращательные). Например, если w = 1, то группа начальных звеньев имеет вид, показанный на рис. 1, a. Если w = 2, то группа начальных звеньев состоит из трёх звеньев (рис. 1, b и c). Практически большинство механизмов имеет w = 1. На начальные звенья ставятся дуговые стрелки, показывающие их движение.

Группу начальных звеньев Ассур назвал механизмом I – го класса I – го порядка.

Группы начальных звеньев

a b c

Рисунок 1

Группы Ассура

Как выяснилось, группой Ассура называется кинематическая цепь, степень подвижности которой равна нулю. Допустим, что в такой цепи имеется: число звеньев – n и число кинематических пар 5 – го класса (по условию – вращательных) – p₅. Заметим, что в группе Ассура все звеньяподвижны, так как неподвижное звено отошло к группе начальных звеньев. Тогда степень подвижности таких групп:

w = 3n – 2p₅ = 0,

откуда получаем следующее соотношение: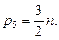

Так как p₅ и n являются натуральными числами, то это уравнение относится к Диофантовым уравнениям, то есть – к алгебраическим уравнениям с рациональными коэффициентами, решения которых отыскиваются в целых числах. Приводим некоторые решения этого уравнения в натуральных числах, заметив, что ноль и отрицательные целые числа не являются натуральными, и в нашем случае не имеющими смысла:

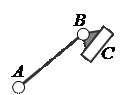
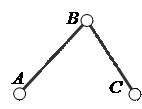
Из первого столбца таблицы видно, что простейшая группа состоит из двух звеньев и трёх кинематических пар 5–го класса (рис. 2). Эта группа относится к группам Ассура второго класса и называется двухповодковой или группой второго порядка. Поводок – это звено группы Ассура, входящее в две кинематические пары, элемент одной пары которых является свободным. Порядок группы всегда определяется количеством свободных элементов кинематических пар. Все группы второго класса являются группами второго порядка.

Группы Ассура второго класса различных видов

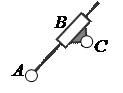
a) первого, b) второго, с) третьего, d) четвёртого, e) пятого.

Рисунок 2

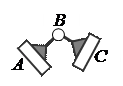
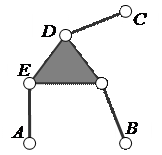
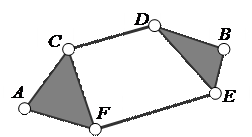
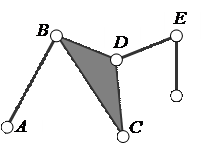
Второй столбец таблицы позволяет образовать три варианта кинематических цепей (рис. 3). Кинематическая цепь, показанная на рис. 3, a, не является группой: она распадается на две группы Ассура второго класса ABC и DEF. Кинематическая цепь, показанная на рис. 3, b, образует группу Ассура третьего класса третьего порядка. В этой группе кинематические пары A, B, C будут внешними, а пары D, E, F – внутренними. Кинематическая цепь, изображённая на рис. 3, c, называется группой Ассура четвёртого класса второго порядка. В этой группе кинематические пары A и B будут внешними, а пары C, D, E, F – внутренними.

Класс группы Ассура выше второго определяется числом внутренних кинематических пар, образующих так называемый исходный контур.

Группы Ассура третьего и более высоких классов по видам не различаются.

Класс механизма определяется наивысшим классом группы Ассура, которая входит в его состав. Следует иметь в виду, что изменением ведущего звена можно либо повысить, либо понизить класс механизма. Поэтому при всех прочих равных условиях класс механизма зависит и от выбора ведущего звена. Кинематический и силовой анализы механизма усложняются с повышением класса механизма, следовательно, всегда надо стремиться выбирать ведущее звено так, чтобы класс механизма оказался наинизшим из всех возможных для данной кинематической схемы механизма.

Три варианта кинематических цепей

F

F

a) две группы Ассура второго класса, b) одна группа третьего класса, c) одна группа четвёртого класса.

Рисунок 3

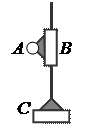
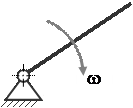
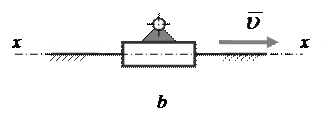
Механизм первого класса представляет собой подвижное звено, образующее со стойкой кинематическую пару пятого класса. В зависимости от того, какая кинематическая пара – вращательная или поступательная – образована, звено совершает относительно стойки вращательное или поступательное движение.

Схемы механизмов первого класса

a) механизм с вращательной парой; b) механизм с поступательной парой

Рисунок 4

Механизм первого класса широко применяется в машиностроении. Так, механизм с вращательной парой является главным механизмом в роторных машинах и приборах – турбинах, электродвигателях, насосах, вентиляторах и т.п. Механизм с поступательной кинематической парой является главным механизмом в двигателях внутреннего сгорания, дизелях, паровых машинах и т.п.

Кинематическая схема механизма второго класса образуется присоединением к механизму первого класса структурных групп звеньев второго класса. При этом законы движения звеньев механизма определяются законом движения механизма первого класса.

Рассмотрим кинематические схемы некоторых механизмов, образованных присоединением одной группы Ассура второго класса различных видов к механизму первого класса. Это четырёхзвенные механизмы с кинематическими парами 5–го класса.

Шарнирный четырёхзвенник включает в себя одну группу Ассура второго класса 1–го вида, присоединённую к ведущему звену и стойке. Схема этого механизма приведена на рис. 5. Механизм образован присоединением к ведущему звену 1 структурной группы звеньев 2 и 3. В точке шарнирного присоединения звена 2 образована вращательная кинематическая пара A, и звено 3 со стойкой 4 образовало вращательную пару C. Звенья 2 и 3 между собой образуют внутреннюю вращательную кинематическую пару B.

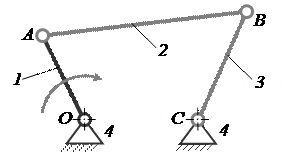Механизм, включающий группу первого вида

Рисунок 5

Кривошипно-ползунный механизм включает в себя одну группу Ассура второго класса 2–го вида, присоединённую к ведущему звену и стойке. Его схема приведена на рис. 6. Механизм образован присоединением к ведущему звену 1 структурной группы звеньев 2 и 3. В точке шарнирного присоединения звена 2 образована вращательная кинематическая пара A, а звено 3 со стойкой 4 образовало поступательную кинематическую пару C. Присоединяемые звенья 2 и 3 между собой образуют внутреннюю вращательную кинематическую пару B.

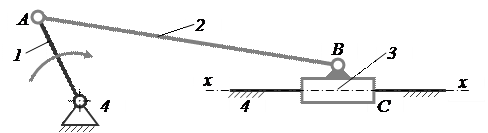Механизм, включающий группу второго вида

Рисунок 6

Кулисный механизм Витворта (Whitworth) включает в себя одну группу Ассура второго класса 3–го вида, присоединённую к ведущему звену и стойке. Его схема приведена на рис. 7. Этот механизм образован присоединением к ведущему звену 1 структурной группы звеньев 2 и 3. В точке шарнирного присоединения звена 2 (кулисного камня) образована вращательная кинематическая пара A, и звено 3 (кулиса) со стойкой 4 тоже образовало вращательную кинематическую пару C. Присоединяемые звенья 2 и 3 между собой образуют внутреннюю поступательную кинематическую пару B.

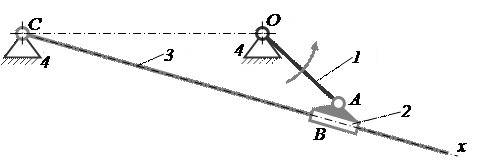Механизм, включающий группу третьего вида

Рисунок 7

Следующий механизм включает в себя одну группу Ассура второго класса 4–го вида, присоединённую к ведущему звену и стойке. Его схема приведена на рис. 8. Этот механизм образован присоединением к ведущему звену 1 структурной группы звеньев 2 и 3. В точке присоединения звена 2 (кулисного камня) образована поступательная кинематическая пара A, и звено 3 (ползун) со стойкой 4 (неподвижной направляющей) тоже образует поступательную кинематическую пару C. Присоединяемые звенья 2 и 3 между собой образуют внутреннюю вращательную кинематическую пару B.

Механизм, включающий группу четвёртого вида

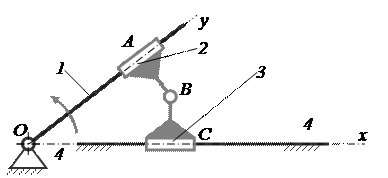
Рисунок 8

Пятый механизм включает в себя одну группу Ассура второго класса 5–го вида, присоединённую к ведущему звену и стойке. Его схема приведена на рис. 9. Этот механизм образован присоединением к ведущему звену 1 структурной группы звеньев 2 и 3. В точке присоединения звена 2 (кулисного камня) образована вращательная кинематическая пара A, и звено 3 (кулиса) со стойкой 4 (неподвижной направляющей) тоже образует поступательную пару C. Присоединяемые звенья 2 и 3 между собой образуют внутреннюю поступательную кинематическую пару B.

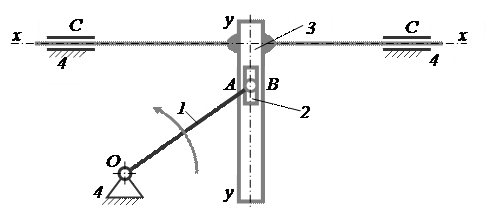Механизм, включающий группу пятого вида

Рисунок 9

Рассмотрим строение шестизвенного механизма второго класса, кинематическая схема которого приведена на рис. 10. Механизм включает в себя две структурные группы Ассура. Звенья 2 и 3 образуют группу 3–го вида, звенья 4, 5 – группу 5–го вида.

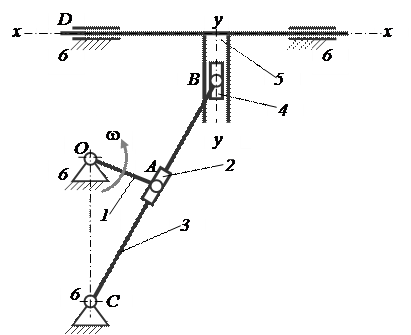Механизм, включающий структурные группы третьего и пятого видов

Рисунок 10

Рассмотрим механизм устройства для отделения (отламывания) чугунных чушек. Это шестизвенный механизм, в котором к начальному механизму присоединена структурная группа Ассура 3–го класса (рис. 11). У рычажного механизма пять подвижных звеньев. Звенья 2, 3, 4 и 5 образуют структурную группу 3–го класса. В точке присоединения звена 2 к кривошипу 1 образована вращательная кинематическая пара A, такие же пары E и D образованы в точке присоединения звена 3 к стойке 6 и звена 4 и к звену 5. Звено 5 со стойкой 6 образуют поступательную кинематическую пару E. Все внутренние вращательные кинематические пары B, C и D образуют исходный контур и определяют класс структурной группы Ассура.

Механизм, включающий одну группу 3–го класса

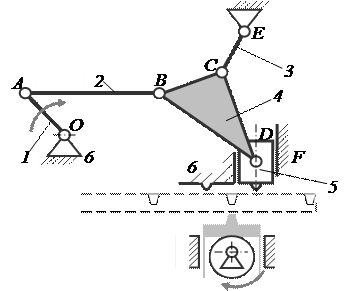Рисунок 11

Ползун 5, приводимый в движение через рычажный механизм от кривошипа 1, надавливает на чушку 6, поджатую столом 8, который предварительно установлен кулачком 7.