Лекция 5. Тема: Замена в плоских механизмах высших пар низшими.

Тема: Замена в плоских механизмах высших пар низшими.

План лекции.

Как известно, плоские механизмы могут иметь звенья, входящие как в низшие, так и в высшие пары. При изучении структуры и кинематики механизмов во многих случаях удобно заменять высшие пары кинематическими цепями или звеньями, входящими только в низшие вращательные и поступательные пары V класса. При этой замене должно удовлетворяться условие, чтобы механизм, полученный после такой замены, обладал прежней степенью свободы и чтобы сохранились относительные в рассматриваемом положении движения всех его звеньев. Рассмотрим трёхзвенный механизм, показанный на рис. 1. Механизм состоит из двух подвижных звеньев 2 и 3, входящих во вращательные пары V класса A и B со стойкой 1 и высшую пару C IV класса, элементы звеньев a и b которой представляют собою окружности радиусов O₂C и O₃C. Согласно формуле (5) степень свободы механизма будет

W = 3 n – 2 p₅ – p₄ = 3×2 – 2×2 – 1 = 1.

Схема механизма с высшей парой в виде двух кругов и заменяющего его механизма шарнирного четырёхзвенника

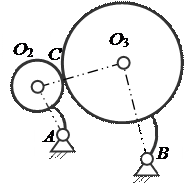Рисунок 1

Можно показать, что рассматриваемый механизм может быть заменён эквивалентным ему механизмом шарнирного четырёхзвенника AO₂O₃B. Высшая пара IV класса в точке C заменяется звеном 4, входящим в точках O₂ и O₃ во вращательные пары V класса. Полученный в результате замены механизм AO₂O₃B называется заменяющим механизмом. Степень свободы W заменяющего механизма будет такой же, что и у заданного механизма. Имеем

W = 3 n – 2 p₅ = 3×3 – 2×4 = 1.

Так как элементы звеньев являются окружностями с центрами в точках O₂ и O₃, то длина O₂O₃ звена 4 оказывается постоянной. Точно также будут постоянными и длины AO₂ и BO₃ звеньев 2 и 3.Заменяющий механизм AO₂O₃B эквивалентен заданному и с точки зрения законов движения звеньев 2 и 3.

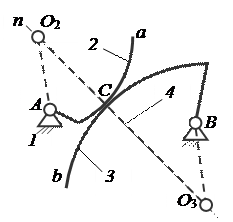
Рассмотренный способ получения заменяющего механизма можно обобщить. Пусть задан механизм с высшей парой, элементы звеньев которой представляют собой произвольно заданные кривые a и b (рис. 2). Для построения схемы заменяющего механизма проводим нормаль nn в точке C касания кривых и отмечаем на ней центры O₂ и O₃ кривизны кривых a и b . По-прежнему центры кривизны O₂ и O₃ сместятся.

Из дифференциальной геометрии известно, что окружность кривизны в точке касания с кривой и сама кривая эквивалентны до производных второго порядка включительно, и поэтому заменяющий механизм эквивалентен основному в такой же степени, т.е. положения, скорости и ускорения одноимённых точек того и другого механизма будут одинаковыми.

Схема механизма с высшей парой, Схема механизма с высшей парой,

элементы звеньев которой – элементы звеньев которой – произвольая

произвольные кривые, и заменя – кривая и прямая, и заменяющего

ющего его механизма шарнирного механизма с тремя вращательными и

четырёхзвенника одной поступательной парами

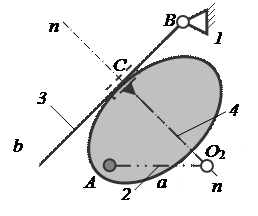Рисунок 2 Рисунок 3

Если один из соприкасающихся элементов будет представлять собой некоторую кривую, а второй – прямую b (рис, 3), то центр кривизны второго профиля будет бесконечно удалён. Условное звено 4 в этом случае будет входить в центре кривизны O₂ элемента 2 во вращательную пару V класса. Вторая вращательная пара, в которую должно входить звено 3, имеет ось вращения бесконечно удалённой и переходит в поступательную пару также V класса.

Далее возможен случай, когда один из соприкасающихся элементов – кривая a, а другой – точка C (рис. 4). В этом случае центр кривизны O₃ элемента C совпадает с самой точкой C, и поэтому условное звено 4 должно входить в две вращательные пары V класса – во вращательную пару с осью, проходящей через центр кривизны O₂ криволинейного элемента a, и во вращательную пару с осью, проходящей через точку C.

Схема механизма с высшей парой, элементы звеньев которой – произвольная

кривая и точка, и заменяющего кривошипно-ползунного механизма

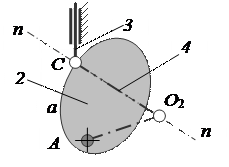Рисунок 4

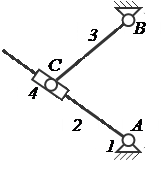
В том случае, когда одним элементом является прямая AC, а другим – точка C (рис. 5), замена сводится к постановке условного звена 4, входящего в одну поступательную и одну вращательную пары. Ось вращательной пары и ось движения поступательной пары должны проходить через точку соприкосновения C. Заменяющий механизм показан на рис. 6.

Элементы звеньев – прямая и точка Схема заменяющего механизма

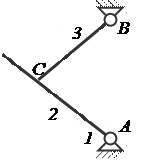Рисунок 5 Рисунок 6

Таким образом, любой плоский механизм с высшими парами IV класса может быть заменён механизмом, в состав которого входят только низшие кинематические пары V класса.

Если все высшие пары IV класса в плоском механизме заменены низшими парами, то структурная формула для заменяющего механизма получит вид

W = 3 n – 2 p₅.