П. 2.6. ДИФФЕРЕНЦИАЛЬНАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ

Возьмем на числовой прямой интервал (х, х + Δх). По формуле (2.5.2) находим

P(x < X <x + Δx) = F(x + Δx) – F(x)

Рис. 2

Определение. Выражение 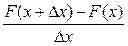называется средней плотностью вероятности случайной величины на интервале [x, x+Δx]

Определение. Предел средней плотности вероятности при Δx→0 называется дифференциальной функцией или плотностью распределения вероятностей непрерывной случайной величины и обозначается f(x),

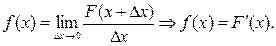
Кривая, соответствующая уравнению y = f(x), называется кривой вероятностей и может иметь вид, изображенный на рис. 2.

Свойства функции f(x).

1°.f(x) ≥ 0 как производная от неубывающей функции.

2°.

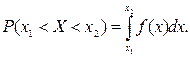(2.6.1)

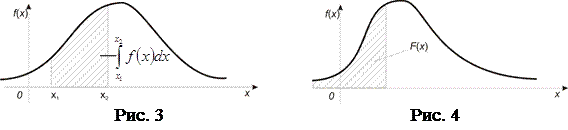
Доказательство. Имеем (рис. 3)

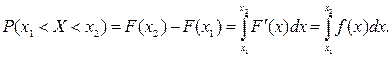
3°.

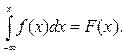(2.6.2)

Доказательство. Имеем (рис. 121)

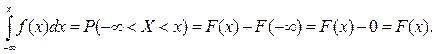(2.6.3)

4°.

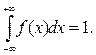(2.6.4)

Доказательство. Находим

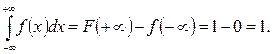
5°. Если возможные значения случайной величины принадлежат замкнутому промежутку, т. е.

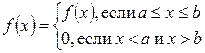
то

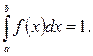(2.6.5)