НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Случайные величины, имеющие нормальное распределение, очень часто встречаются в земледелии и животноводстве, ветеринарии, инженерном деле и в других отраслях знания. Приведем примеры таких величин:
1. масса клубня картофеля;
2. масса одного зерна пшеницы некоторого сорта;
3. содержание жира в молоке, полученного от различных животных;
4. содержание кормовых единиц в суточном рационе шестимесячных телок;
5. масса животного некоторой породы на определенную дату;
6. погрешности измерений.
Для этих величин характерным является то, что на их формирование влияет большое число факторов, причем влияние каждого из них мало и ни один фактор не имеет значительного преимущества перед другими. Эти величины можно отнести к величинам, имеющим нормальный закон распределения, полагая, что их возможные значения не отрицательны.
Определение. Случайная величина X имеет нормальный закон распределения, если ее функция плотности вероятности имеет вид
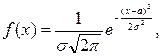 (2.8.1)
(2.8.1)
где σ и а - параметры распределения.
График функции f (x) называется кривой нормального распределения. Методами дифференциального исчисления можно установить, что:
1) кривая симметрична относительно прямой х = а;
2) функция имеет максимум при х = а,
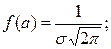
3) по мере удаления х от точки а функция убывает и при х → ±¥ кривая приближается к оси Ох;
4) кривая выпукла при 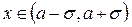 и вогнута при
и вогнута при 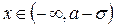 и при
и при 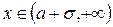 . График функции f (x) имеет вид, изображенный на рис. 5.
. График функции f (x) имеет вид, изображенный на рис. 5.
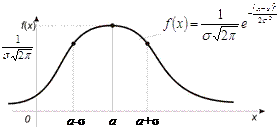 Форма кривой изменяется с изменением параметра σ. С возрастанием σ функция f (x) убывает, кривая становится более пологой и растянутой вдоль оси Ох.
Форма кривой изменяется с изменением параметра σ. С возрастанием σ функция f (x) убывает, кривая становится более пологой и растянутой вдоль оси Ох.
Рис. 5
Значениям случайной величины, близким к математическому ожиданию, соответствует большая плотность вероятности, т. е. малые отклонения значений случайной величины от ее математического ожидания встречаются более часто, чем большие.
Параметр а есть математическое ожидание случайной величины, а σ - среднее квадратическое отклонение.
Пример 1. Известно, что случайная величина X подчинена нормальному закону распределения, М(Х) = 6, σ2 = 9. Найдите функцию плотности вероятности.
Решение. Имеем а = 6, а = 3:
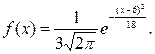
Пример 2. Известно, что случайная величина X подчиняется нормальному закону с функцией плотности вероятности
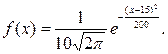
Найдите М(Х) и D(X).
Решение. Имеем M(X) = 15, D(X) = σ2 = 102 = 100.
Дата добавления: 2015-09-21; просмотров: 864;
