ЗАДАЧИ И УПРАЖНЕНИЯ

1. В коробке 150 яблок. Из них 3 яблока поражены болезнью в явной форме. Чему равна относительная частота появления пораженного яблока?

2. Относительная частота появления клубней картофеля, имеющих механические повреждения при уборке, равна 0,15. В корзине 350 клубней. Сколько клубней окажется поврежденными?

3. Известно, что всхожесть пшеницы составляет 90%. Сколько необходимо взять зерен, чтобы взошло 360 растений?

4. Всхожесть семян дикой яблони равна 60%. Сколько потребуется высеять семян, чтобы получить 120 ростков?

5. Для определения всхожести пшеницы посеяли две серии по 200 зерен. Получено соответственно 189 и 193 всхода. 1) Какова относительная частота всхожести в каждой серии? 2) Чему равна процентная всхожесть пшеницы?

6. В стаде 200 коров, из них 90 не превышают трехлетнего возраста. Наудачу отбирается одно животное. Найдите вероятность того, что возраст коровы не менее 3 лет.

7. На молочном комплексе 10% коров имеют удой свыше3600 кг, 25% коров - от 2800 до 3600 кг, остальные - менее2800 кг. Определите вероятность того, что удой наудачу выбранной коровы свыше 2800 кг.

8. В двух отсеках зернохранилища находится посевной материал (пшеница). Семена первого отсека имеют всхожесть 80%,второго-85%. Отбирается по 1 зерну из каждого отсека. Найдите вероятности следующих событий: А - оба зерна дадут всходы; В - одно зерно взойдет, а другое - нет; С - оба зерна не дадут всходов. Проверьте равенство

1. Р(А)+Р(В)+Р(С)=1.

10. Из 5 лучших в хозяйстве свиноматок надо выбрать трех для выставки. Сколькими способами можно сделать выбор?

11. Исследователь зафиксировал результаты полевого опыта с 20 делянок и внес результаты в ЭВМ. При распечатке ведомости результаты «смешались».

12. Найдите вероятность того, что при этом каждой делянке соответствует верный результат.

13. Какова вероятность того, что для 19 делянок в распечатке указан верный результат?

14. В хозяйстве 5 участков земли, которые необходимо занять под 5 культур. Какова вероятность того, что произвольное закрепление культур за участками совпадает с запланированным?

15. Эффективность некоторой вакцины в формировании иммунитета составляет 75%. Вакцинировалось два животных. Пусть A₁ и А₂ - события, состоящие в том, что соответственно первой второе животное приобрели иммунитет. Найдите вероятность следующих событий: А = {оба животных приобрели иммунитет} В = {одно животное приобрело иммунитет}; С = {ни одно животное не приобрело иммунитет}, D ={хотя бы одно животное приобрело иммунитет}. Являются ли зависимыми события: А₁ и А₂, А₁ 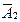и , и ?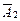

16. Вероятность рождения бычка или телочки при отеле принята равной 0,5. Сколько раз должна телиться корова, чтобы с вероятностью 0,9 иметь хотя бы одну телочку?

17. Некоторая популяция растений состоит из особей трех типов, помеченных АА, Аа, аа. Численность каждого типа составляет соответственно 200, 600 и 50. Из популяции выбирают одно растение. Найдите вероятности событий:

а) выбранное растение принадлежит к типу АА;

б) выбранное растение принадлежит к типу АА или Аа.

18. В клетке 6 белых и 4 серые мыши. Случайно отбирают 3 мышей, не возвращая обратно. Вычислите вероятности событий:A = {все три мыши белые}; В = {две белые и одна серая}; С = {две серые и одна белая}; D = {все три серые}.

19. Для некоторой местности среднее число солнечных дней в июле составляет 25. Найдите вероятность того, что первые3 дня июля солнечные.

20. В корзине 12 плодов. Из них 3 поражены болезнью в скрытой форме. Из корзины последовательно извлекают два плода. Вычислите:

вероятность того, что первый взятый плод больной;

вероятность того, что второй вынутый плод будет больным при условии, если первый оказался здоровым.

21. В ящике 30 яблок. Из них 3 поражены болезнью в скрытой форме. Последовательно без возвращения достают 3 яблока. Какова вероятность того, что они здоровы?

22. В корзине 12 яблок, из них 4 сорта А, остальные сорта В. Взяли 3 яблока. Найдите вероятность следующих событий:

событие C₁= {среди взятых 3 яблока сорта А};

событие С₂ = {взято 3 яблока сорта В};

событие С₃ = {взято 2 яблока сорта А и одно сорта В}.

23. Коэффициент использования рабочего времени (относительное время) двух комбайнов соответственно равен 0,8 и 0,6. Учитывая, что остановки в работе каждого комбайна случайны и независимы одна от другой, определите относительное время:

совместной работы комбайнов;

работы только одного комбайна;

простоя обоих комбайнов

24. Коэффициент использования рабочего времени у 3 тракторов соответственно равен 0,8, 0,7 и 0,6. Учитывая, что остановки в работе каждого трактора случайны и независимы одна oт другой, найдите относительное время.

совместной работы всех тракторов;

совместной работы двух тракторов,

работы только одного трактора;

простоя всех тракторов.

25. Вдоль длинных стен животноводческого комплекса проложено два транспортера, работающих независимо. Предположим, что вероятность безотказной работы каждого из них в течение дня равна 0,9. Определите вероятность безотказной работы обоих транспортеров:

а) в течение одного дня,

б) в течение ближайших шести дней.

26. У шести животных имеется заболевание, причем вероятность выздоровления равна 0,98. Какова вероятность того, что: а) выздоровят все шестеро животных; б) не выздоровит ни одного, в) выздоровят только пятеро?

27. Вероятность события = {одно посеянное зерно пшеницы не прорастет} равна 0,009. Какова вероятность события = {из1000 семян не прорастет: а) равно 8?}; б) = {не более 5 семян?};в) = {не менее 5 семян}?

28. В хозяйстве имеется 6 гусеничных и 4 колесных трактора Вероятность события = {за время выполнения некоторой работы гусеничный трактор не выйдет из строя} равна 0,95, а для колесного трактора эта вероятность равна 0,8. Для выполнения некоторой работы произвольно выбирается трактор. Найдите вероятность события = {до завершения работы трактор не выйдет из строя}.

29. В трех корзинах находится картофель В первой 10%поврежденных клубней, во второй -15%, в третьей - 10%. Из наудачу выбранной корзины берут один клубень. Какова вероятность события = {клубень не поврежден}?

30. Предприятия L, M, N производят соответственно 25, 30 и 45% запасных частей одного наименования к доильным аппаратам, которые поступают на центральную базу. Доля брака для них составляет соответственно 1, 2 и 3%. Взятое наугад изделие оказалось бракованным. Вычислите вероятности тою, что оно сделано на предприятии L, на предприятии М, на предприятии N.

1. В зерне, предназначенном для очистки, 10 % сорняков. Наудачу отобраны 4 зерна. Напишите биномиальный закон распределения дискретной случайной величины X (числа сорняков среди 4 отобранных зерен) и постройте многоугольник распределения.
2. В среднем на 1 м² посева встречается 0,5 растений сорняков. Найдите вероятность события = {на площади 5 м² окажется: ровно один сорняк}; (не окажется ни одного сорняка}.
3. Доля поражения зерна вредителями в скрытой форме составляет 0,002. а) Составьте закон распределения случайной величины X-числа зараженных зерен среди 500 отобранных, б) Найдите наивероятнейшее число пораженных зерен среди 500 отобранных.
4. Определите среднее число солнечных дней на протяжении недели, если для данной местности вероятность того, что каждый день будет солнечным, составляет 0,6.
5. При изучении характера распределения сеялкой семян подлине рядка установлено, что на 20 из 100 двухсантиметровых отрезков было по 3 шт. семян, на 40 – по 2 шт., на 30 – по1 зерну, а на остальных семян вообще не оказалось. Найдите М(Х) и D(X) случайной величины X – числа семян на двухсантиметровом отрезке, приняв относительные частоты за вероятности.

36.Найдите М (Х) и D (X), приняв относительные частоты появления случайной величины X за вероятности.

37.Найдите М(Х) и D(X), приняв относительные частоты за вероятности.

38.Случайная величина X задана плотностью распределения f (х) = 2 sin 4x: в интервале [0, π/4], вне этого интервала f (х) = 0. Найдите вероятность события – {X попадет: а) в интервал [π/6; π/4]; б) в интервал [π/2; π]; в) в интервал [0, π/8].

39.Составьте дифференциальную функцию для нормально распределенной случайной величины и постройте ее график, если даны ее параметры: 1) М (Х) = 4, σ_х = 0,2, 2) М (Х) = –0,5, σ_x = 2; 3) М (Х) = 3, σ_x = 1/4; 4) М (Х) = 0, σ_x = 1.

40.Случайная величина X-масса одного зерна – распределена нормально. Математическое ожидание массы зерна равно 0,18 г, среднее квадратичное отклонение 0,05. Хорошие всходы дают зерна, масса которых больше, чем 0,15 г. Найдите: а) процент семян, которые дадут хорошие всходы; б) величину, которую с вероятностью 0,95 не превысит масса отобранного зерна.

41.Норма высева на 1 га равна 150 кг. Фактический расход на 1 га колеблется около этого значения. Случайные отклонения характеризуются средним квадратическим отклонением в 10 кг.. Полагая, что норма высева – случайная величина с нормальным распределением, найдите: 1) вероятность события = {расход семян на 100 га не превысит 15,1 т}; 2) массу семян, которая обеспечивает посев площади в 100 га с вероятностью 0,95.

42.Методом проб установлено, что потери зерна при уборке в среднем составляют 3 г на 1 м²; среднее квадратическое отклонение равно 1 г. Найдите. 1) вероятность события = {на 1 га потери составят не менее чем 29,8 кг}; 2) величину, которую с вероятностью 0,99 не превысят потери на 1 га. Считать, что X (потери зерна) есть нормально распределенная случайная величина.

43.Средняя масса плодов в одном ящике равна 10 кг, а среднее квадратическое отклонение в массе плодов одного ящика 1,5 кг. Найдите: 1) вероятность события = {в 100 ящиках масса плодов окажется не менее 970 кг}; 2) наибольшее значение, которое с вероятностью 0,95 не превзойдет масса 100 ящиков.

44.Принять во внимание, что масса плодов в одном ящике - нормально распределенная случайная величина.