П. 2.3. БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Пусть случайная величина X есть число k появлений события А при п независимых испытаниях. Вероятность появления события А в каждом испытании постоянна и равна р. Возможные значения случайной величины X числа 0, 1, 2, 3, ..., n. Вероятности появления каждого из этих значений в силу независимости испытаний определяют по формуле Бернулли:

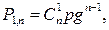
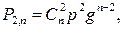
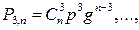
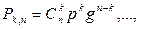
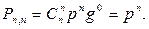
Эти же вероятности можно получить, если воспользоваться формулой бинома Ньютона

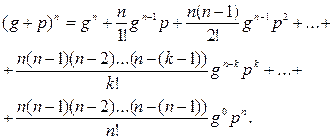
Но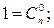

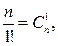
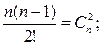
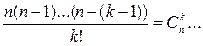
Определение. Закон распределения дискретной случайной величины называется биномиальным, если вероятности возможных ее значений равны соответствующим членам разложения бинома (g+p)ⁿ.

Математическое ожидание биномиального распределения равно

M (X) = np. (2.3.1.)

Дисперсия случайной величины X, распределенной по биномиальному закону, равна npg:

D(X) = npg. (2.3.2)