П. 2.4. РАСПРЕДЕЛЕНИЕ ПУАССОНА

Задача 1. Вероятность того, что зерно пшеницы не прорастет, принимается равной 0,01. Какова вероятность того, что из 500 посеянных семян не дадут всходов ровно 8 семян? Не более чем 5 семян?

В этой задаче число семян, не давших всходы - дискретные случайные величины. Заметим, что число испытаний п в задаче велико, а вероятность появления события в каждом испытании мала. Возможные значения случайной величины указать нетрудно, это x₁ = 0, x₂ = 1, x₃ = 2, ..., x₅₀₁ = 500. Вероятность наступления события A k раз, когда п велико, а р мало, определяют по формуле Пуассона, впервые исследовавшего эту задачу:

(2.4.1)

где а - математическое ожидание случайной величины (а = пр); k – число появлений события A (k может принимать только целочисленные значения, теоретически неограниченные, k ≤ n).

Определение. Закон распределения дискретной случайной величины, когда вероятности возможных ее значений находятся по формуле Пуассона (2.4.1), называется распределением Пуассона.

Можно доказать, что для случайной величины X, распределенной по закону Пуассона, ее математическое ожидание равно дисперсии. Это свойство применяется в статистике.

Вернемся к приведенной выше задаче.

1. Имеем п = 500, р = 0,01, g = l – p = 0,99; а = пр = 500∙0,01 = 5. По таблице находим

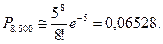
Вероятность P_8,500 мала. Вероятность того, что не взойдет не более чем 5 семян, равна

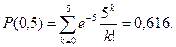
Вероятность того, что не взойдет более пяти семян

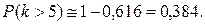
В случае биномиального распределения случайной величины, когда математическое ожидание мало отличается от дисперсии, т. е. когда np ≈ npg, при решении задач пользуются распределением Пуассона, для данной функции имеются таблицы.