Характеристические числа и характеристические векторы

От характеристических векторов зависят динамические свойства системы. Рассмотрим векторное уравнение

y = Ax,

где у – вектор входа (n×1); x – вектор выхода (n×1); А – квадратная матрица (n×n).

Вопрос о нахождении характеристических значений связан с вопросом: существует ли такой вектор x, который в результате его преобразования с помощью матрицы А переходит в вектор y, имеющий то же направление в пространстве что и вектор x. Если такой вектор x существует, то это значит, что yпропорционален x(рис. 2.11):

y = Ax = λx,

где λ – скаляр.

Рис. 2.11. Характеристический вектор y= λx

Перенесем λx = λExв левую часть:

(λE – A)x= 0,

где E – единичная матрица.

Это векторно-матричное уравнение можно записать в виде равносильной системы скалярных уравнений, соответствующих строкам матрицы А:

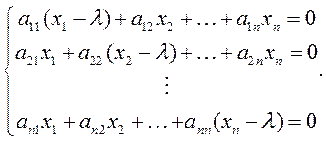
Данная система имеет нетривиальное решение в том случае, если определитель матрицы коэффициентов равен нулю:

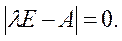
Раскрытие данного определителя приводит к характеристическому уравнению:

.

Многочлен n-й степени относительно l называется характеристическим многочленомматрицы А.Корни этого уравнения равны характеристическим (собственным) значениям матрицы А. Особый интерес представляют коэффициенты многочлена а₁ и а_n.

Если положить λ = 0, то:

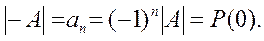
Представим

и снова положим, что λ = 0. Тогда

,

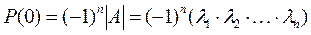откуда

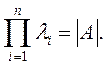
Таким образом, произведение характеристических чисел равно определителю матрицы А. В случае равенства нулю какого-нибудь из характеристических чисел матрица А становится особенной (вырожденной).

Раскрывая характеристическое уравнение, записанное в виде произведения сомножителей, можно выразить коэффициенты при различных степенях λ через характеристические числа.

Выразим коэффициент при λ^n-1:

С другой стороны, раскрывая также определитель |λE–A|, найдем, что коэффициент при λ^n-1 равен со знаком минус сумме диагональных элементов матрицы А:

Таким образом, сумма диагональных элементов квадратной матрицы равна сумме ее характеристических чисел:

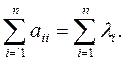
Ввиду важности этого свойства сумме диагональных элементов матрицы присвоено особое название: след матрицы. Обозначим след матрицы: