Определитель Грама

Определитель Грамастроится для системы векторов в предположении, что векторы x_i линейно зависимы:

.

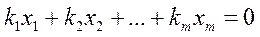Запишем последовательно скалярные произведения векторов x_i :

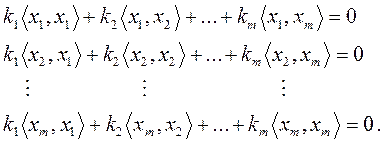
Известно, что система однородных уравнений (в данном случае относительно неизвестных k_i) имеет нетривиальное решение только в том случае, если определитель матрицы с коэффициентами <x_i , x_j> равен нулю. Этот определитель и называется определителем Грама:

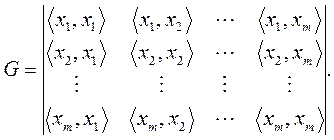
В результате можно сделать следующий вывод.

Системавекторовx₁,…, x_mлинейно независимав том случае, когдаопределитель Грамане равен нулю.

В том случае, когда x₁,…, x_m –система ортогональных векторов, определитель Грамаприобретает диагональный вид.

Вопросы к разделу 2.5

1. В чем состоит условие ортогональности векторов?
2. Результатом скалярного произведения двух векторов является скаляр, а результатом векторного произведения?
3. Почему неравенство 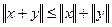называется неравенством треугольника?
4. Почему в неравенстве Шварца 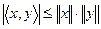в левой части используются одинарные прямые вертикальные скобки, а в правой – двойные?
5. Что называется дефектом особенной матрицы?
6. Что такое ранг матрицы?
7. Какие векторы являются линейно независимыми?
8. Что можно сказать о системе векторов, для которой определитель Грама равен нулю?
9. Что можно сказать о системе векторов, для которой определитель Грама имеет диагональный вид?