Адаптивна система керування високоточним електроприводом з мінімізацією середньо квадратичної похибки
Використання пошукових методів оптимізації розглянемо на прикладі адаптивної системи керування високоточним електроприводом. Основна частина системи (рис.6.4) виконана за імпульсно - фазовим принципом керування з розділенням каналів фазового та частотного керування за допомогою нелінійного логічного блоку (НЛБ) й аналогового ключа (АК).
Адаптивне керування застосовується для автоматичного переналагодження параметрів системи таким чином, щоб для кожного з можливих режимів роботи при широкому діапазоні регулювання швидкості та навантаження отримати мінімальні динамічні похибки. Основні впливи на систему, до яких можна віднести перешкоди вимірювання координат руху, зміни моменту опору, параметричні збурення в електродвигуні та кінематичній передачі, мають виражену залежність від швидкості електроприводу й механізму.
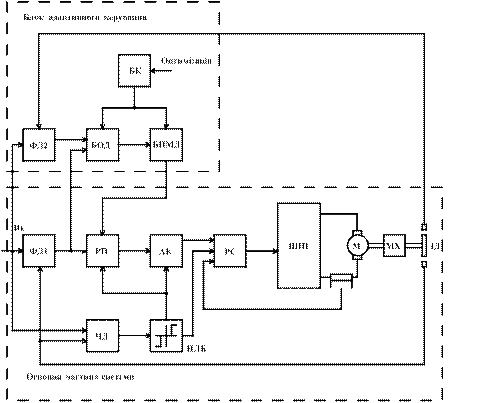
Рис.6.4. Функціональна схема адаптивної системи керування високоточним електроприводом
Зміни у спектральному складі впливів при широкому регулюванні швидкості можуть статись настільки значними, що мінімальна динамічна похибка буде забезпечуватись лише на одному рівні швидкості. У разі зміни швидкості відхилення від мінімальної похибки буде дуже суттєвим. Пошукова адаптивна система виконує в цьому випадку автоматичну оптимізацію на кожному рівні швидкості у заданому діапазоні її регулювання.
Використовуючи у прецизійній системі електроприводу високочастотний широтно – імпульсний перетворювач (ШІП), можна замикати контур регулювання струму на частотах, при яких ефективно фільтруються параметричні збурення в електродвигуні. Тоді основними збуреннями у системі будуть зміни моменту опору на валу механізму 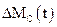 та перешкоди імпульсного давача ІД
та перешкоди імпульсного давача ІД 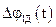 .
.
Оптимізація імпульсно – фазової системи керування зводиться до динамічного синтезу регулятора положення (РП) за умови мінімуму середньоквадратичної похибки ( або дисперсії похибки). Використовуючи нормовані амплітудно – частотні характеристики системи типу (- 3 -1 -2) та визначаючи із параметричного синтезу системи частоту зрізу 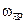 й частоти спрягання характеристик системи, можна переконатись у тому, що при адаптивній автоматичній оптимізації можна змінювати тільки частоту зрізу, зберігаючи при цьому співвідношення частот спрягання відносно неї незмінним. Залежності дисперсії кутової
й частоти спрягання характеристик системи, можна переконатись у тому, що при адаптивній автоматичній оптимізації можна змінювати тільки частоту зрізу, зберігаючи при цьому співвідношення частот спрягання відносно неї незмінним. Залежності дисперсії кутової 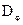 або швидкісної
або швидкісної 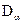 похибок від
похибок від 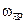 , що визначаються частотними характеристиками та енергетичними спектрами впливів, мають при однаковій формі ЛАЧХ ярко виражені мінімуми. Оптимальні частоти зрізу залежать від швидкості механізму та режиму навантаження (рис.6.5)
, що визначаються частотними характеристиками та енергетичними спектрами впливів, мають при однаковій формі ЛАЧХ ярко виражені мінімуми. Оптимальні частоти зрізу залежать від швидкості механізму та режиму навантаження (рис.6.5)
В адаптивній системі керування прецизійним електроприводом (рис.6.4) допоміжна підсистема пошуку екстремуму здійснює пошук оптимальної частоти зрізу, яка забезпечує мінімізацію дисперсії кутової або швидкісної похибки у широкому діапазоні змін швидкості двигуна та навантаження. З цією метою у систему вводяться блоки обчислення дисперсії (БОД) та пошуку мінімуму дисперсії (БПМД) похибки системи, керування якими у режимі автоматичної оптимізації здійснюється від блоку керування (БК).
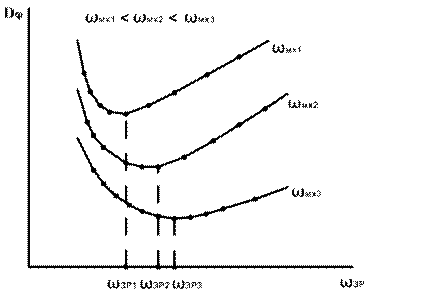
Рис.6.5. Залежність оптимальної частоти зрізу від швидкості та режиму навантаження
Для вимірювання дисперсії дійсної кутової або швидкісної похибки необхідно виключити завади вимірювання кута, що зумовлені неточністю нанесення рисок на лімбу давача. З цією метою використовуються два зміщених відносно один одного за обертом лімбу пристрою вимірювання фазового неузгодження, який складається з двох фотооптичних систем та двох фазових дискримінаторів ФД1 та ФД2, працюючих у синфазному режимі. Структурна схема блоку обчислення дисперсії дійсної кутової похибки наведена на рис.6.6. Вихідні напруги 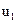 та
та 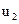 підсилювачів 1 й 2 зв`язані з дійсною кутовою похибкою механізму
підсилювачів 1 й 2 зв`язані з дійсною кутовою похибкою механізму 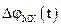 співвідношеннями
співвідношеннями
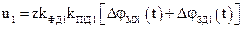 ;
;
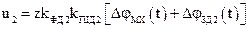 ,
,
де 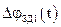 ,
, 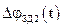 - завади давача по двох пристроях вимірювання;
- завади давача по двох пристроях вимірювання; 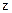 - дискретність давача;
- дискретність давача; 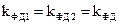 - коефіцієнти передачі фазових дискримінаторів;
- коефіцієнти передачі фазових дискримінаторів; 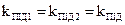 - коефіцієнти передачі підсилювачів.
- коефіцієнти передачі підсилювачів.
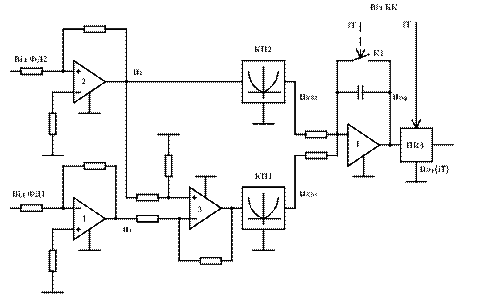
Рис.6.6. Структурна схема блоку обчислення дисперсії дійсної кутової похибки
Коли дві фотоелектричні системи рознесені на кут, при якому кореляційна функція 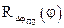 похибки давача обертається в нуль, то завади
похибки давача обертається в нуль, то завади 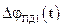 та
та 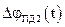 стають взаємно некорельованими. Відсутня також кореляція між
стають взаємно некорельованими. Відсутня також кореляція між 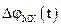 та
та 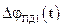 ,
, 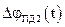 . Середні квадрати величин
. Середні квадрати величин 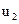 та
та 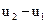 знаходяться за виразами
знаходяться за виразами
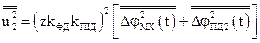 ;
;
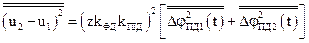 .
.
Враховуючи, що завади 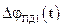 та
та 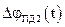 відносяться до одного й того ж стаціонарного процесу, маємо
відносяться до одного й того ж стаціонарного процесу, маємо 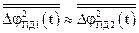 . На підставі наведених виразів можна записати
. На підставі наведених виразів можна записати
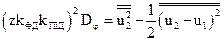 ,
,
де 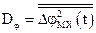 - дисперсія дійсної кутової похибки системи.
- дисперсія дійсної кутової похибки системи.
Обчислення дисперсії похибки за останнім виразом здійснюється за допомогою сумуючого підсилювача 3 (рис.6.6), двох квадратичних перетворювачів КП1, КП2 та інтегратора зі сталою часу 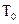 , який виконує усереднення сигналу за кінцевий інтервал часу
, який виконує усереднення сигналу за кінцевий інтервал часу 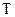 . Пристрій вибірки – зберігання (ПВЗ) призначений для запам`ятовування за час
. Пристрій вибірки – зберігання (ПВЗ) призначений для запам`ятовування за час 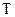 сигналу
сигналу 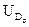 . Після запам`ятовування
. Після запам`ятовування 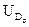 короткочасним замиканням інтегратора ключем К1 здійснюється установка його в нуль. Керування інтегратором та ПВЗ здійснюється від генератора тактів, який розташований в БК.
короткочасним замиканням інтегратора ключем К1 здійснюється установка його в нуль. Керування інтегратором та ПВЗ здійснюється від генератора тактів, який розташований в БК.
При вимірюванні дисперсії дійсної похибки за швидкістю 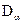 масштабні підсилювачі 1 та 2 мають бути замінені двома ідентичними диференціюючими підсилювачами.
масштабні підсилювачі 1 та 2 мають бути замінені двома ідентичними диференціюючими підсилювачами.
З врахуванням коефіцієнтів передачі квадратичних перетворювачів 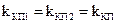 та інтегратора
та інтегратора 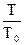 напруги на виході БОД та дисперсії
напруги на виході БОД та дисперсії 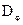 ,
, 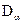 кутової й швидкісної похибок зв’язані між собою співвідношеннями
кутової й швидкісної похибок зв’язані між собою співвідношеннями
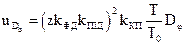 ;
;
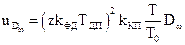 ,
,
де 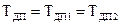 - сталі часу диференціюючих підсилювачів.
- сталі часу диференціюючих підсилювачів.
З метою швидкого виходу поблизу екстремуму та відстежування його дрейфуючого положення у підсистемі пошуку мінімуму дисперсії дійсної похибки використаний комбінований алгоритм пошуку з переналагодженням поблизу екстремуму алгоритму методу дихотомії на кроковий автоколивальний алгоритм.
Вибір цього алгоритму пошуку зумовлений такими міркуваннями. Крутість кривих 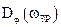 (рис. 6.5) суттєво залежить від швидкості механізму
(рис. 6.5) суттєво залежить від швидкості механізму 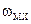 та відхилення частоти
та відхилення частоти 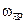 від оптимальних значень. Тому градієнтні алгоритми не забезпечують швидкого збігання процесу пошуку при широкому діапазоні регулювання швидкості та навантаження. У той же час геометричні методи, наприклад, метод дихотомії, забезпечують найменші витрати часу на пошук екстремуму. Для відстежування дрейфу екстремуму здійснюється перемикання системи на кроковий алгоритм пошуку із суміщенням пробних та робочих кроків.
від оптимальних значень. Тому градієнтні алгоритми не забезпечують швидкого збігання процесу пошуку при широкому діапазоні регулювання швидкості та навантаження. У той же час геометричні методи, наприклад, метод дихотомії, забезпечують найменші витрати часу на пошук екстремуму. Для відстежування дрейфу екстремуму здійснюється перемикання системи на кроковий алгоритм пошуку із суміщенням пробних та робочих кроків.
Переналагодження параметрів основної частини системи здійснюється шляхом зміни параметрів РП (рис.6.7).
Нехтуючи пружними зв’язками в електроприводі та представляючи замкнений контур регулювання струму без інерційною ланкою 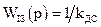 , можна записати передавальну функцію розімкненого контуру положення з врахуванням переналагоджуваних параметрів у наступному вигляді:
, можна записати передавальну функцію розімкненого контуру положення з врахуванням переналагоджуваних параметрів у наступному вигляді:
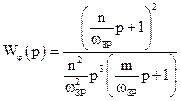 ,
,
де 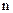 ,
, 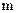 - коефіцієнти;
- коефіцієнти; 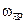 - частота зрізу.
- частота зрізу.
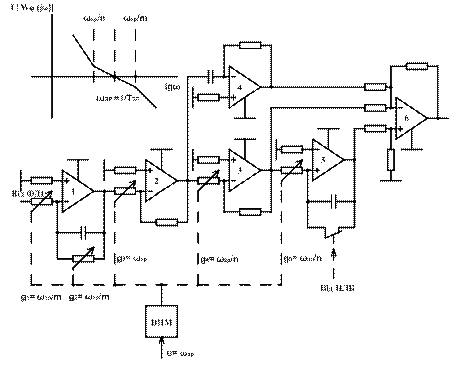
Рис. 6.7. Схема для зміни параметрів регулятора положення адаптивної системи керування
Відповідно до цієї передавальної функції ЛАЧХ наведена на рис. 6.7. Приймаючи до уваги, що передавальна функція незмінної частини системи дорівнює
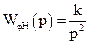 ,
,
де 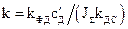 , а передавальна функція регулятора положення
, а передавальна функція регулятора положення
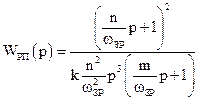 .
.
Схема РП (рис.6.7) відповідає цьому перетвореному виразу з врахуванням технічної можливості переналагодження параметрів за допомогою ШІМ. Переналагодження здійснюється дією на резистори РП таким чином, щоб зміна їх провідностей призводила до зміни частоти зрізу 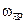 системи та зберігала сталими співвідношення спрягаючих частот
системи та зберігала сталими співвідношення спрягаючих частот 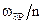 та
та 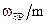 .
.
Дата добавления: 2015-09-18; просмотров: 1448;
