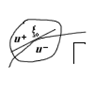Лемма Шварца.
Теорема (об устранимой особенности). Если 1) Функция f – непрерывна в некоторой окрестности точки z0, т.е. в круге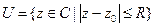 
.
2) Функция f – голоморфна в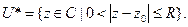 
То функция f – голоморфна в 
.
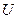Доказательство. Пусть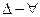 
замкнутый 
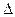, лежащий в 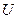. Рассмотрим случаи:
1. 
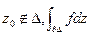(по ИТК)=0 2. 
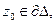проведём дугу окружности радиуса 
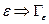3. 
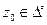
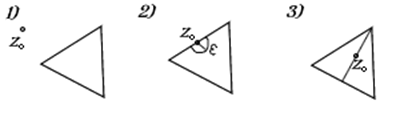
2. 
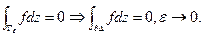
3. Сводится ко 2-му разбиением на 2 части. Далее f –непрерывна в U и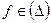 
в U. Следовательно по теореме Мореры f – голоморфна в U.
Лемма Шварца. Если 1) f – голоморфна в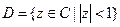 
2) 
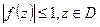3) 
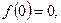
То 1) выполняются неравенства: а)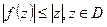 
б) 
2) Если в неравенстве а) достигается равенство хотя бы в одной точке отличной от 0, имеем: в неравенстве б) достигается равенство, то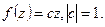 
Доказательство. Определим функцию 
. Очевидно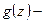 
голоморфна в 
. 
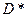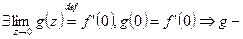непрерывна в D. Тогда 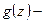голоморфна в D по теореме об устранимой особенности. Зафиксируем 
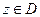, проведём окружность 
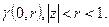Применим принцип мах модуля: 
. Мы доказали неравенства а) и б). Теперь пусть выполняется посылка 2) утверждения,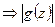 
достигает мах в D, 
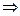по принципу мах модуля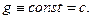 
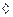
Следствие.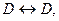 
конформно, следовательно ДЛО.
|
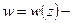берём такое отображение. Тогда 
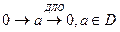так можно сделать. Тогда без ограничения общности считаем, что 
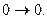Тогда к w можно применить лемму Шварца к обратному (и к прямому тоже 
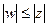), отображению 
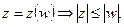А тогда 
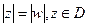и снова применим лемму Шварца, получим 
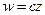, а это ДЛО.
ФОРМУЛА СОХОЦКОГО
Дата добавления: 2015-09-02; просмотров: 1469;