Постановка задачи.

Пусть Г – простая спрямляемая кривая, f – функция непрерывная на Г. 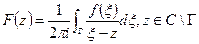(интеграл типа Коши). Зафиксируем точку 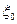на Г. Пусть она отлична от концов кривой.

Определение. Точка 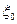называется правильной точкой кривой Г, если в этой точке существует касательная к кривой.

Считаем далее, что 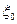- правильная. 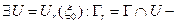простая дуга (без самопересечений). Кривая разбивает U на 2 области: U+ лежит слева от кривой и U^- справа. Обозначим: 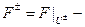ограничения.

Задача. Вычислить граничные значения.

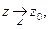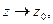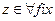Определение. не касательным способом, если и сектору с углом < 180⁰.

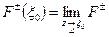(z) докажем существование этих пределов и вычислим их.

Определение. Пусть число 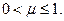Будем говорить, что f удовлетворяет условию Гёльдера с показателем 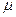в точке 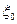, если выполняется неравенство: 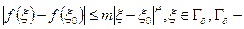некотороя окрестность.

Замечание. На протяжении всего параграфа полагаем, что f удовлетворяет условию Гёльдера.