Принципы максимального модуля.
Теорема о среднем.
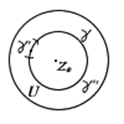
Теорема. Если функция  голоморфна в круге
голоморфна в круге 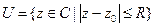 , то её значение в центре круга = среднему арифметическому её значений на границе, т.е.
, то её значение в центре круга = среднему арифметическому её значений на границе, т.е. 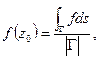 где
где 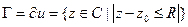 - окружность.
- окружность.
Доказательство. Напишем формулу Коши: 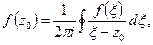 параметрический вид окружности:
параметрический вид окружности: 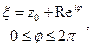 тогда
тогда 
Принципы максимального модуля.
Теорема. Если 1) f – голоморфна в D
2) 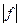 достигает мах в D, то
достигает мах в D, то 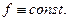
Доказательство. 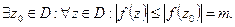 2 случая: 1. m = 0, тогда f = 0,
2 случая: 1. m = 0, тогда f = 0, 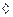
2. m > 0. Рассмотрим множество Е: 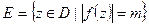 .
.
Свойства Е: 1) Во-первых, оно не пусто: 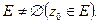
2) Во-вторых, Е замкнуто относительно D (следует из того, что  непрерывна относительно D).
непрерывна относительно D).
3) В-третьих, Е – открытое.
|
 тогда
тогда 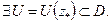 Докажем:
Докажем: 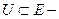 открытое. Некоторое
открытое. Некоторое 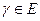 . Доказать, что каждая такая
. Доказать, что каждая такая 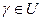 предположим обратное, т.е.
предположим обратное, т.е. 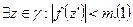
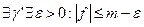 на
на 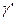 и
и 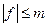 на
на 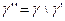 . Напишем теорему о среднем:
. Напишем теорему о среднем:
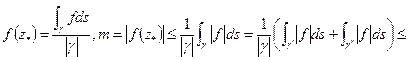
|
 противоречие, таким образом,
противоречие, таким образом,
предположение (1) неверное. 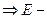 открытое.
открытое.
Т.к. D – связанное и из 1),2),3) 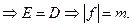
Далее рассмотрим: 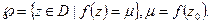
Свойства 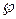 : 1) Оно не пусто:
: 1) Оно не пусто: 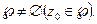
2) 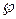 замкнуто относительно D (непрерывность f).
замкнуто относительно D (непрерывность f).
3) 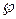 – открытое.
– открытое.
Докажем 3) свойство. Возьмём 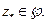
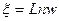 , где Ln –непрерывная ветвь логарифма, а
, где Ln –непрерывная ветвь логарифма, а 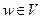 .
. 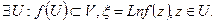 (композиция голоморфна).
(композиция голоморфна). 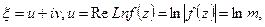 поэтому
поэтому 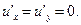 Тогда из условия Коши-Римана следует
Тогда из условия Коши-Римана следует 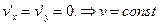 в круге
в круге 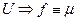 в круге
в круге 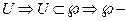 открытое. Аналогично,
открытое. Аналогично, 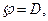 таким образом,
таким образом, 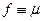 в D.
в D. 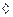
Следствие. Если 1) D – ограниченная область с границей Г.
2) f - а) голоморфна в D б) непрерывна в D, тогда 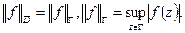
Т.е. здесь сказано, что мах достигается на границе.
Вопрос: Справедлив ли принцип минимального модуля?
Ответ: а) Вообще говоря – нет.
б) если 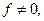 то – да.
то – да.
Т.к. если функция имеет нули, то в нулях – минимум следовательно а) доказано, а если функция не имеет нулей, то можно рассмотреть функцию 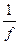 , а для неё работает теорема о принципе мах модуля.
, а для неё работает теорема о принципе мах модуля.
Дата добавления: 2015-09-02; просмотров: 780;