Лемма Жордана.
|
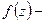 голоморфная в
голоморфная в 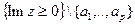 , где
, где 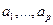 - конечное число особых точек принадлежащих
- конечное число особых точек принадлежащих 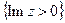 , Обозначим:
, Обозначим: 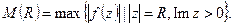 Предположим, что
Предположим, что 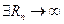 (последовательность чисел), т.ч.
(последовательность чисел), т.ч. 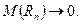 Пусть
Пусть 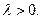 Тогда утверждается, что интеграл Фурье:
Тогда утверждается, что интеграл Фурье: 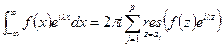 , если интеграл слева существует в смысле главного значения по Коши.
, если интеграл слева существует в смысле главного значения по Коши.
Доказательство. Обозначим интеграл за J. А правую часть равенства за А.
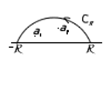
Обозначим 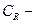 замкнутый контур. Пусть R – достаточно большое, т.ч.
замкнутый контур. Пусть R – достаточно большое, т.ч.
Все 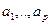 лежат внутри замкнутого контура. Тогда по основной теореме Коши о вычетах:
лежат внутри замкнутого контура. Тогда по основной теореме Коши о вычетах: 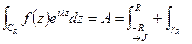 при
при 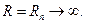 Если докажем, что
Если докажем, что 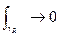 , тогда лемма доказана. Оценим:
, тогда лемма доказана. Оценим: 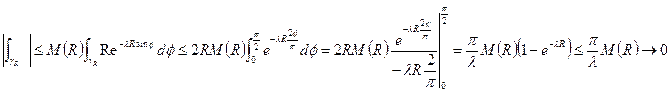 При
При 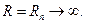 Важно, что
Важно, что 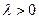 иначе не верно.
иначе не верно. 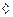
Лемма верна для той полуплоскости, где exp убывает.
Пример. 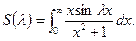
|
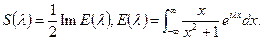 Возьмём
Возьмём 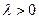 и
и 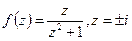 - полюс 1ого порядка. По лемме Жордана пишем ответ:
- полюс 1ого порядка. По лемме Жордана пишем ответ: 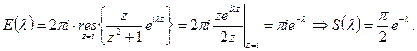 Верно для
Верно для 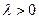 .
.
Для 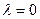
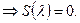
Для 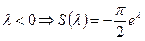 в силу нечётности. Тогда
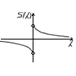
в силу нечётности. Тогда 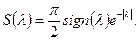 График:
График:
Задача. Рассмотрим: 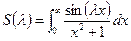 . Исследовать поведение
. Исследовать поведение 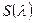 при
при 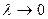 . (можно дифференцировать по параметру
. (можно дифференцировать по параметру 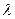 . Обоснование!!!).
. Обоснование!!!).
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
Дата добавления: 2015-09-02; просмотров: 1500;