Доказательство. Предположим противное. Пусть характеристическая функция множества R2:

Предположим противное. Пусть характеристическая функция множества R₂:

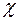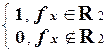(x) = является вычислимой.

Рассмотрим вспомогательную функцию g(x), задаваемую соотношениями:

g(0) = mt( 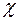(t) = 0);

g(k+1) = mt( 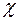(t) = 0 & t > g(k)).

Так как 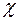вычислимая функция, то функция g также вычислимая.

Последовательность функций f_g(0), . . . , f_g(i), . . . содержит все всюду определенные функции последовательности (3) в порядке возрастания номеров этих функций в нумерации p, множества F¹.

Пусть h(x, y) - определенная ранее универсальная функция.

Тогда функция q(x, y) = h(g(x), y) является вычислимой, и для каждого фиксированного значения x справедливо следующее равенство: q(x, y) = f_g(x)(y).

Поэтому функция d, определяемая соотношением: d(x) = q(x, x)+1 также является вычислимой всюду определенной частично-рекурсивной функцией. Поскольку последовательность f_g(0), . . . , f_g(i), . . . содержит все всюду определенные частично-рекурсивные функции, то $ i Î N(d(x) = f_g(i)(x)).

Рассмотрим значение d(i).

1.По определению функции d справедливы равенства:

d(i)= q(i, i)+1 = f_g(i)(i)+1.

2.С другой стороны значение i выбрано так, что

d (i) = f_g(i)(i).

Полученное противоречие означает, что R₂ не является разрешимым множеством.