ОПРЕДЕЛЕНИЕ. Множество A называется разрешимым множеством, если его характеристическая функция является вычислимой.

Множество A называется разрешимым множеством, если его характеристическая функция является вычислимой.

Очевидно, что разрешимость множества A означает существование алгоритма, который для произвольного элемента aÎN^k за конечное число шагов работы дает ответ на вопрос о принадлежности a множеству A.

Пример. Множество {n|n - четное число} является рекурсивным множеством, поскольку имеет рекурсивную характеристическую функцию f(x) = 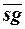(mod(x, 2)).

Здесь mod(x, 2) -функция остатка от деления x на 2.

Упражнение. Пусть A и B разрешимые подмножества множества N^k. Показать, что множества A È B, A Ç B и N^k \ A также являются разрешимыми.

Покажем, что существование алгоритма решения произвольной задачи, исходные данные и решения которой представляются целыми неотрицательными числами, связано с разрешимостью специального множества натуральных чисел.

Увеличим числовые представления всех возможных решений задачи на 1. Это позволяет выделить 0 из множества решений задачи в качестве специального значения.

Произвольной задаче T поставим в соответствие множество

D_T= {(a, b) | ((b ¹ 0) & (решение задачи T для начальных данных a равно b)) Ú ((b = 0) & (решение задачи T для начальных данных a не существует))}.

Заметим, что на некоторых начальных данных задача может не иметь решения. При этом отсутствие решения задачи означает не только отсутствие решения, что может считаться отрицательным решением, а неопределенность значения решения или его отсутствия.

Покажем, что для задачи T существует алгоритм получения решения при любых начальных данных тогда и только тогда, когда D_TÍ N² является разрешимым множеством.

1.Пусть для T имеется разрешающий алгоритм A. Тогда для проверки принадлежности пары (a, b) множеству D_T достаточно применить A к начальному данному a и сравнить полученное решение c со значением b-1.

2.Пусть D_TÍ N². Тогда нахождение решения T для начального данного a состоит в проверке того, что (a, 0) ÏD_T. Если проверяемое условие имеет место, то решение задачи T существует и может быть найдено последовательной проверкой выполнения условия (a, i) Î D_T для i = 1, 2, . . . , выполняемой до тех пор пока не будет найдена пара (a, b) Î D_T , озгачающая, что решение T на начальных данных a равно b-1.

Рассмотрим три специальные задачи, относящиеся к свойствам программ в произвольном универсальном языке программирования.