Доказательство. Предположим противное. Пусть характеристическая функция множества R1: (x1, x2)= является вычислимой.

Предположим противное. Пусть характеристическая функция множества R₁: 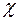(x₁, x₂)= 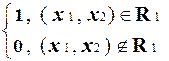является вычислимой.

Поскольку 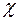- вычислимая, то вычислима и функция

g(x) = 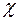(x, x).

Определим вспомогательную функцию:

d(x) = .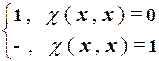

Функция d называется диагональной. Для каждого значения своего аргумента, равного x, она определена тогда и только тогда, когда значение f_x(x) не определено.

То есть d отлична от любой функции последовательности (3) всех одноместных частично-рекурсивных функций.

С другой стороны d получается из вычислимой числовой функции 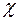с помощью программно реализуемых (вычислимых) операций и поэтому является вычислимой.

Следовательно, d должна совпадать с одной из функций в последовательности всех одноместных частично-рекурсивных функций (3).

Полученное противоречие означает, что предположение о разрешимости множества R₁ является неверным.

Следовательно, R₁ - это неразрешимое множество.