Доказательство. Пусть языки U1и U2 распознаются автоматами

Пусть языки U₁и U₂ распознаются автоматами

Â₁ = (A, Q₁, j₁, q₀, D₁) и Â₂ = (A, Q₂, j₂, q₁, D₂).

Построим конечный автомат Á, который функционирует из своего начального состояния так же, как и два параллельно работающих автомата Â₁ и Â₂.

Определим автомат Á как (A, Q₁ 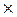Q₂, j, (q₀, q₁), D), где Dобозначает множество состояний, которое будет выбираться так, чтобы обеспечить распознавание множеств U₁È U₂, U₁Ç U₂, и U₁\ U₂.

Состояния Á - это пары (q_i, q_j), где q_i ÎQ₁ и q_j ÎQ₂. Начальным состоянием Á является состояние (q₀, q₁). Функция перехода j представляет собой пару функций (j₁, j₂), каждая из которых определяет значение соответствующей компоненты состояния Á. То есть, если в момент времени t автомат находится в состоянии (q¢(t), q²(t)), то значение состояния Á в момент t+1 равно (j₁(x(t), q¢(t)), j₂(x(t), q²(t))).

Тогда автомат Áиз начального состояния (q₀, q₁) распознает множество U₁ È U₂, если в качестве множества распознающих состояний Dвыбрано множество

D₁ 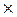Q₂ È Q₁ 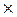D₂.

Действительно, при переработке произвольного входного слова 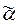из начального состояния (q₀, q₁) компоненты состояния автомата Á изменяются так же, как состояния автоматов Â₁ и Â₂, когда эти автоматы перерабатывают 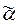из состояний q₀ и q₁ соответственно.

Поэтому Á заканчивает переработку 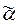в состоянии из D тогда и только тогда, когда автомат Â₁ заканчивает переработку 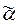в состоянии из D₁ или Â₂ заканчивает переработку этого же слова в состоянии из D₂.

То есть 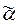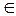U₁ È U₂ 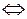Áзаканчивает переработку этого слова в состоянии из множества D₁ 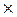Q₂ È Q₁ 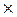D₂.

Аналогично можно показать, что если в качестве множества распознающих состояний взять D₁ 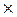D₂, то автомат Á из начального состояния (q₀, q₁) распознает U₁Ç U₂.

Множество U₁\ U₂ распознается конечным автоматом Á, для которого D = D₁ 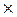(Q₂ \ D₂).

Если множество слов U распознается автоматом

 = (A, Q, j, q₀, D), то A^* \ U распознается автоматом

(A, Q, j, q₀, Q \ D).