ОПРЕДЕЛЕНИЕ. Множество U A*распознается автоматом Â из начального состояния q0и множества D Q- распознающих состояний
Множество U 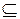 A*распознается автоматом Â из начального состояния q0и множества D
A*распознается автоматом Â из начального состояния q0и множества D 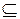 Q- распознающих состояний, если
Q- распознающих состояний, если
" 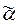 Î A*(
Î A*( 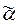 Î U
Î U 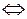 Â распознает
 распознает 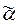 ).
).
Например. Если A = {o, s}, то множество слов в этом алфавите, имеющих вид: 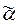 1 sos
1 sos 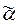 2, где
2, где 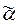 1 и
1 и 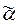 2 - это произвольные слова из A*, распознается автоматом, изображенным на рис.7.10.В приведенной на этом рисунке диаграмме не отображены сведения о значениях вункции выхода автомата, поскольку они не влияют на процесс распознавания
2 - это произвольные слова из A*, распознается автоматом, изображенным на рис.7.10.В приведенной на этом рисунке диаграмме не отображены сведения о значениях вункции выхода автомата, поскольку они не влияют на процесс распознавания
 о
о
q0
s o s, o
s q1 q3
o q2 s
Рис.7.10
Здесь q0 - начальное состояние автомата, а {q3} - множество распознающих состояний.
Состояние q0 соответствует ситуации, когда поступившая на вход автомата часть перерабатываемого слова не заканчивается никаким началом слова вида sos 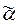 2.
2.
Тогда состояние q1 соответствует ситуации, когда последний поступивший на вход символ может быть первым в слове sos, q2 соответствует случаю, когда два последних символа это so. Наконец, q3 соответствует случаю, когда на входе автомата уже появились последовательно все символы слова sos .
Заметим, что для распознавания слов конечными автоматами значения символов на выходе автомата несущественны.
Поэтому в диаграмме из приведенного примера дуги не размечены значениями выходных символов.
В дальнейшем автомат Â = (A, B, Q, j, y), который распознает множество слов U из начального состояния q0 для множества распознающих состояний D, будем записывать как Â = (A, Q, j, q0, D).
Если некоторое множество U 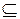 A*распознается некоторым конечным автоматом, то U называется автоматным языком.
A*распознается некоторым конечным автоматом, то U называется автоматным языком.
Дата добавления: 2015-09-18; просмотров: 615;
