Композиция автоматов

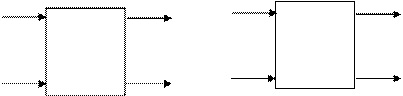
Пусть заданы автоматы Â₁ и Â₂, имеющие соответственно m₁ и m₂ входов, а также n₁ и n₂ выходов (рис.7.11).

x₁ y₁ x₁y₁

. . . Â₁ . . . Â₂

x_m1 y_n1 x_{m 2} y_n2

Рис. 7.11

Пусть k - такое целое число, что k 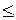n₁ и k 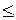m₂.

Тогда композицией Â₁ и Â₂ называется автомат, который получается из Â₁ и Â₂ подсоединением k различных выходов Â₁ к k различным входам Â₂.

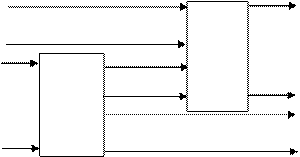
Например, так как это выполнено для случая, изображенного на рис.7.12.

. . . Â₂

. . .

Â₁. . .

. . .

. . .

Рис. 7.12

Понятно, что функционирование полученного устройства является корректным, если символы, появляющиеся на выходах Â₁ и поступающие на входы Â₂ принадлежат одному и тому же алфавиту.

Для простоты будем считать, что множества символов, появляющихся на любых входах и выходах автоматов всегда являются символами одного и того же алфавита.

Упражнение. Определить число выходов композиции автоматов Â₁ и Â₂в указанных ранее условиях.

Если автоматы Â₁ и Â₂ имеют по одному входу и одному выходу, то композиция таких автоматов, изображенная на рис. 7.13, называется суперпозицией Â и Â₂.

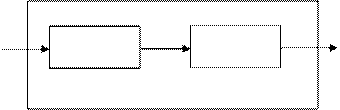Â₁ Â₂

Â

Рис. 7.13

Пусть заданы два автомата Â₁ = (A, A, Q₁, j₁, y₁) и Â₂ = (A, A, Q₂, j₂, y₂).

Суперпозиция этих автоматов представляет собой автомат

 = (A, A, Q₁ Q₂, j, y), т.е. множество состояний автомата  - это множество пар (q_i, q_j), где q_i ÎQ₁ и q_j ÎQ₂.

Пусть начальные состояния автоматов Â₁ и Â₂ - это соответственно q⁰ и q^l.

Выпишем канонические уравнения для автомата Â:

q₁(t₀) = q⁰;

q₂(t₀) = q^l;

q₁(t+1) = j₁(x(t), q₁(t));

q₂(t+1) = j₂(y₁(x(t), q₁(t)), q₂(t));

y(t) = y₂(y₁(x(t), q₁(t)), q₂(t)).

То есть y = y₂(y₁(x(t), q₁(t)), q₂(t)), где x(t) - это символ на входе Â₁, а q₁(t) и q₂(t) - состояния Â₁ и Â₂ в момент t. Функция перехода j представляет собой пару функций, определяющих первую и вторую компоненты состояния Âв следующий момент времени.