Доказательство. Пусть rk = rk+1. Покажем, что rk+1 = rk+2

Пусть r_k = r_k+1. Покажем, что r_k+1 = r_k+2. То есть если состояния q_i и q_j являются (k + 1)-неотличимыми, то они являются и (k+ 2)-неотличимыми.

Пусть a 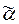- это произвольное входное слово длины k+ 2, начинающееся с символа a. Тогда после переработки первого символа этого слова из состояний q_i и q_j как начальных автомат Á переходит в новые состояния q_i1 и q_j1, которые являются k-неотличимыми.

Так как r_k = r_k+1и q_i1 r_k q_j1, то по условию леммы q_i1 r_k+1q_j1. Поэтому слово 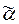из состояний q_i1 и q_j1 будет перерабатываться в одно и то же выходное слово. Следовательно, произвольное входное слово a 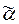из состояний q_i1 и q_j1 перерабатывается в одно и то же выходное слово.

Следовательно, q_i и q_j являются k+2-неотличимыми.

Поэтому r_k+1= r_k+2.

Повторяя проведенные рассуждения, можно показать, что r_k+1 = r_k+2 = r_k+3 = r_k+4 . . .

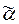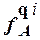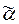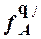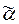Следовательно, для любого входного слова значения ( ) и ( ) равны, т.е. q_i и q_j являются неотличимыми состояниями.

Поэтому, если состояния q_i и q_j неотличимы на словах длины k, то они неотличимы на словах любой конечной длины, т.е. q_i и q_j являются неотличимыми.

Следовательно, r_k = e.