Доказательство.

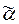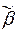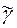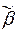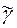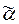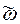Пусть = ( )^¥, где = a_i1, ... , a_ik и = a_j1, ... , a_jp, и автомат Á перерабатывает в из начального состояния q₀.

Обозначим начальный момент времени как t₀.

Рассмотрим последовательность q₁, q₂, . . . , q_i, . . . - (1)

состояний автомата Á в моменты времени:

t₀+k, t₀+k+p, . . . , t₀ + k+ (i - 1)p, . . .

То есть это моменты времени, в которые на вход Á поступают первые символы первого, второго, . . . , i-го, . . . вхождений периода 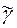во входное сверхслово .

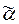Поскольку множество состояний Á является конечным, то в последовательности состояний (1) имеются одинаковые состояния. Пусть это q_s и q_r, где s < r.

Тогда Á, начав работу в состоянии q_s, заканчивает переработку слова ( 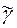)^r-s переходом в исходное состояние. Следовательно, следующее слово ( 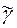)^r-s в слове ( 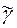)^¥ этот автомат перерабатывает так же, как и предыдущее такое слово.

Представим 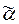в виде 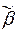( 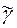)^{s - 1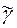}(( )^{r- s})^¥.

Тогда при переработке 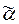из начального состояния q₀ последовательно идущие вхождения слова ( 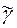)^r-s в части (( 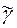)^{r- s})^¥.перерабатывается автоматом в одинаковые фрагменты выходного сверхслова. Последнее утверждение верно, поскольку такая переработка всякий раз начинается из одного и того же состояния.

Следовательно, автомат Á перерабатывает 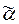в периодическое сверхслово

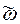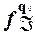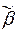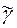= ( ( )^{s - 1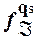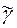})( (( )^{r - s}))^¥.