ТЕОРЕМА 7. 2
Числовая функция f(x, y) = xy не вычисляется конечными автоматами.
Доказательство
Предположим противное. Пусть существует конечный автомат Á= (A, B, Q, j, y), который из начального состояния q0 вычисляет f.
Здесь A = {00, 01, 10, 11}, B= {0, 1} и Q = {q1, . . . , qk}.
Пусть перемножаются два числа, большее из которых представляется в двоичной системе записью длины d. Тогда длина произведения двух таких чисел может достигать длины 2d-1. При этом, если представлять такие произведения двоичными записями длины 2d-1, то первыеd компонент в них могут быть любыми двоичными последовательностями длины d.
Будем считать, что перемножаемые числа x и y, большее из которых представляется двоичной записью длины d, пополняются незначащими нулями и записываются в виде наборов длины 2d-1.
Перемножаемые числа поступают на вход Á в виде последовательности пар значений одноименных двоичных разрядов, начиная с младших разрядов.
Пусть 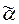 - входное слово автомата Á, представляющее два перемножаемых числа x и y. Автомат заканчивает переработку первых d символов
- входное слово автомата Á, представляющее два перемножаемых числа x и y. Автомат заканчивает переработку первых d символов 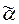 в некотором состоянии qi.
в некотором состоянии qi.
После этого на вход Á поступают остальные символы 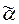 в виде последовательности d-1 пар нулей.
в виде последовательности d-1 пар нулей.
Значения появляющихся при этом символов на выходе автомата образуют слово длины d-1, определяемое только состоянием qi.
Поэтому значения первых d разрядов произведений произвольных чисел длины d могут принимать не более k различных значений.
Поэтому для любого значения dдолжно выполняться неравенство: k³ 2d-1.
Поскольку значение k является фиксированным, а d - произвольное, то последнее неравенство неверно.
Следовательно, предположение о существовании автомата Á, вычисляющего функцию умножения пар чисел, неверно.
Доказательство окончено.
Упражнение.
1. Доказать, что для любого фиксированного натурального числа n существует конечный автомат, вычисляющий функцию f(x) = n ´ x;
2. Доказать, что не существует конечного автомата, вычисляющего функцию f(x, y) = div(x,y).
Имеет место еще одно свойство, ограничивающее вычислительные возможности автоматов, следующее из конечности множеств состояний.
Пусть A = {a1, ... , an} - некоторый алфавит. Всякая бесконечная последовательность 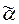 символов этого алфавита называется сверхсловом в A.Множество всех сверхслов в алфавите A обозначается как
символов этого алфавита называется сверхсловом в A.Множество всех сверхслов в алфавите A обозначается как 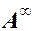 .
.
Сверхслово 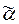 называется периодическим, если оно может быть представлено в виде:
называется периодическим, если оно может быть представлено в виде: 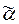 =
= 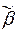 (
( 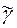 )¥. Здесь
)¥. Здесь 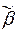 и
и 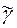 - слова в алфавите A. Сверхслово
- слова в алфавите A. Сверхслово 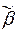 (
( 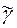 )¥ получается сцеплением слова
)¥ получается сцеплением слова 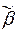 и сверхслова (
и сверхслова ( 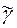 )¥, получаемого последовательным выписыванием
)¥, получаемого последовательным выписыванием 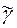 бесконечное число раз. Слово
бесконечное число раз. Слово 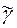 называется периодом, а (
называется периодом, а ( 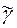 )¥ - периодической частью сверхслова
)¥ - периодической частью сверхслова 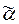 .
.
Если автомат Á в момент t0находится в начальном состоянииq0 и в моменты времени t0, t0+1, . . . на его вход поступают символы сверхслова 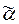 , то в эти же моменты времени на выходе Áпоявляются символы выходного алфавита, образующие выходное сверхслово
, то в эти же моменты времени на выходе Áпоявляются символы выходного алфавита, образующие выходное сверхслово 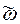 .
.
В этом случае будем говорить, что Á из начального состояния q0 перерабатывает входное сверхслово 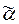 в выходное сверхслово
в выходное сверхслово 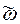 .
.
Дата добавления: 2015-09-18; просмотров: 859;
