Пара сил. Момент пары сил

Парой сил называют систему двух равных по модулю сил, направленных вдоль параллельных прямых в противоположных направлениях (рис. 2.2). Плоскость, в которой размещены силы пары, – это плоскость действия пары сил, а кратчайшее расстояние d между линиями действия сил называется плечом пара.

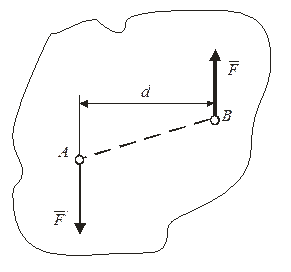
Рисунок 2.2

Силы пары не составляют уравновешенную систему сил, потому что не имеют общей линии действия, и не сводятся к равнодействующей, так как их геометрическая сумма равняется нулю. Действие пары сил сводится к вращательному эффекту, который характеризуется моментом пары.

Момент пары (алгебраический) – это взятая с соответствующим знаком величина, равная произведению модуля одной из сил пары на плечо пары:

. (16)

Алгебраический момент пары сил будет положительным, если пара сил пытается вращать тело против хода часовой стрелки.

В соответствии с определением, алгебраический момент пары сил численно равняется площади параллелограмма, построенного на силах пары (рис. 2.3):

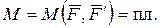
АВСD = 2пл. АВС = 2пл. АВD.

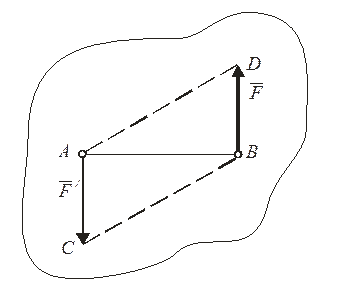
Рисунок 2.3

Пары сил в плоскости имеют такие свойства:

а) Действие пары сил на твердое тело полностью определяется моментом пары сил;

б) пару сил можно как угодно поворачивать и переносить в любое место плоскости действия пары;

в) у пары сил можно изменять плечо и величину силы, сохраняя неизменными направление ее поворота, величину момента и плоскость действия пары;

г) система любого количества пар сил в плоскости эквивалентна одной паре сил, лежащей в той же плоскости, момент которой равен алгебраической сумме моментов данных пар, т.е. пары сил, лежащие в одной плоскости, складываются алгебраически.

Условия равновесия пар сил – для равновесия системы пар необходимо и достаточно, чтобы момент результирующей пары сил равнялся нулю.

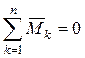2.1.3 Теорема о параллельном переносе силы: силу можно переносить параллельно самой себе в любую точку твердого тела в плоскости, добавляя при этом пару сил, момент которой равен моменту переносимой силы относительно новой точки ее приложения.

а ) б) в)

Рисунок 2.4

Доказательство теоремы осуществляется поэтапно (рис. 2.4):

- к действующей на тело в точке А силе 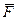(рис. 2.4, а) добавляют в точке переноса В уравновешенную систему сил 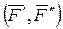~ 0, выбрав силы 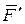и 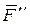равными по величине силе 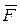(рис 2.4,б);

- рассматривая совокупность сил 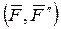как пару сил с моментом 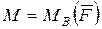, убедиться, что действие на тело силы 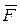в точке А (рис. 2,4,а) и системы сил 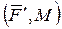(рис. 2,4,в) тождественно