Приведение системы сил на плоскости к простейшему виду
Основная теорема статики о приведении произвольной системы сил к заданному центру: Любая плоская система сил эквивалентна одной силе, равной главному вектору системы 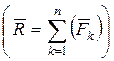 , приложенному в некоторой точке (центре приведения) и паре сил, момент которой равен главному моменту сил системы относительно центра приведения
, приложенному в некоторой точке (центре приведения) и паре сил, момент которой равен главному моменту сил системы относительно центра приведения 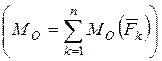 .
.
Доказательство теоремы выполняется в такой последовательности: выбирают некоторую точку (например, точку О)в качестве центра приведения и переносят каждую силу 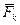 в эту точку, добавляя, согласно теореме о параллельном переносе силы, соответствующие пары сил
в эту точку, добавляя, согласно теореме о параллельном переносе силы, соответствующие пары сил  . В результате этого получают систему сходящихся сил
. В результате этого получают систему сходящихся сил 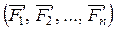 , приложенных в точке О, где
, приложенных в точке О, где 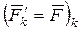 , и систему добавленных пар сил
, и систему добавленных пар сил 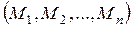 , моменты которых
, моменты которых 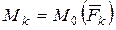 . Затем заменяют систему сходящихся сил
. Затем заменяют систему сходящихся сил 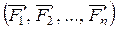 равнодействующей, равной главному вектору системы
равнодействующей, равной главному вектору системы 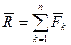 , а систему пар сил
, а систему пар сил 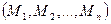 – одной парой сил с моментом, равным главному моменту
– одной парой сил с моментом, равным главному моменту 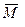 системы относительно центра приведения. В результате получают, что
системы относительно центра приведения. В результате получают, что  ~
~ 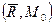 . Следовательно, теорема доказана.
. Следовательно, теорема доказана.
Случаи приведения пространственной системы сил к простейшему виду:
1 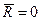 , а
, а 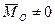 – система сводится к одной паре сил с моментом, равным главному моменту системы, и значение главного момента системы от выбора центра приведения не зависит.
– система сводится к одной паре сил с моментом, равным главному моменту системы, и значение главного момента системы от выбора центра приведения не зависит.
2  , а
, а 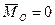 – система сил приводится к равнодействующей, равной главному вектору системы, линия действия которой проходит через центр О приведения.
– система сил приводится к равнодействующей, равной главному вектору системы, линия действия которой проходит через центр О приведения.
3  , и
, и  –такая система сил сводится к одной равнодействующей
–такая система сил сводится к одной равнодействующей 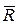 , равной главному вектору системы, линия действия которой смещена от предыдущего центра приведения на расстояние
, равной главному вектору системы, линия действия которой смещена от предыдущего центра приведения на расстояние 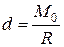 .
.
4 Если главный вектор  и главный момент
и главный момент  , то система сил будет уравновешенной, т.е.
, то система сил будет уравновешенной, т.е. 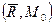 ~0.
~0.
2.1.5 Условия равновесия плоской системы сил
Необходимые и достаточные условия равновесия любой плоской системы сил определяются уравнениями:
 .
.
Величина главного вектора плоской системы сил определяется зависимостями:  , а главного момента – зависимостью
, а главного момента – зависимостью 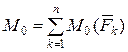 .
.
Главный вектор 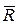 будет равняться нулю только тогда, когда одновременно
будет равняться нулю только тогда, когда одновременно  . Следовательно, условия равновесия выполняются при выполнении таких аналитических уравнений:
. Следовательно, условия равновесия выполняются при выполнении таких аналитических уравнений:
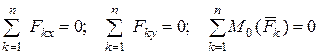 .
.
Эти уравнения являются основной (первой) формой аналитических условий равновесия произвольной плоской системы сил, которые формулируются так: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и алгебраическая сумма моментов этих сил относительно любой точки на плоскости действия сил равнялись нулю.
Отметим, что число уравнений равновесия произвольной плоской системы сил в общем случае равняется трём. Они могут быть представлены в разной форме.
Существуют еще две формы уравнений равновесия произвольной плоской системы сил, выполнение которых выражает условия равновесия ().
Вторая форма аналитических условий равновесия предусматривает: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех сил относительно двух точек и сумма проекций этих сил на ось, неперпендикулярную к прямой, проведенной через эти точки равнялись нулю:
 .
.
(линия АВ неперпендикулярна оси Ох)
Сформулируем третью форму аналитических условий равновесия рассматриваемой системы сил: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов сил системы относительно любых трех точек, не лежащих на одной прямой, равнялись нулю:
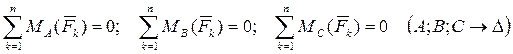 .
.
В случае плоской системы параллельных сил, можно направить ось Оу параллельно силам системы. Тогда проекции каждой из сил системы на ось Ох будут равняться нулю. В итоге для плоской системы параллельных сил останутся две формы условий равновесия.
Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы сумма проекций всех сил на параллельную им ось и сумма моментов всех сил относительно любой точки равнялись нулю:
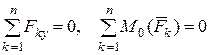 . ()
. ()
Эта первая форма аналитических условий равновесия для плоской системы параллельных сил вытекает из уравнений ().
Вторую форму условий равновесия плоской системы параллельных сил получим из уравнений ().
Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы сумма моментов всех сил системы относительно двух точек, которые не лежат на прямой, параллельной силам, равнялись нулю:
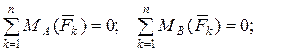 (AB
(AB 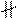
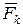 ). ()
). ()
Дата добавления: 2015-09-14; просмотров: 1057;
