Пример 2.1
Однородная балка 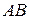 (рис. 2.6, а) весом G=1 кH, к которой в точке
(рис. 2.6, а) весом G=1 кH, к которой в точке 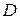 на расстоянии
на расстоянии 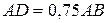 подвешен груз Р весом 2 кН, закреплена в точке А с помощью неподвижного шарнира и удерживается в состоянии равновесия под углом α=45º к вертикали закрепленной в точке В нитью, переброшенной через неподвижный блок Е с подвешенным на ее конце грузом Q. Определить опорные реакции шарнира А и вес груза Q, если наклон нити к вертикали составляет угол
подвешен груз Р весом 2 кН, закреплена в точке А с помощью неподвижного шарнира и удерживается в состоянии равновесия под углом α=45º к вертикали закрепленной в точке В нитью, переброшенной через неподвижный блок Е с подвешенным на ее конце грузом Q. Определить опорные реакции шарнира А и вес груза Q, если наклон нити к вертикали составляет угол 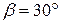 .
.
Решение
Рассмотрим равновесие балки, на которую действуют активные силы 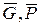 и сила
и сила 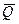 , приложенная в точке
, приложенная в точке 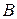 и направленная вдоль нити (см. рис. 2.6, б).
и направленная вдоль нити (см. рис. 2.6, б).
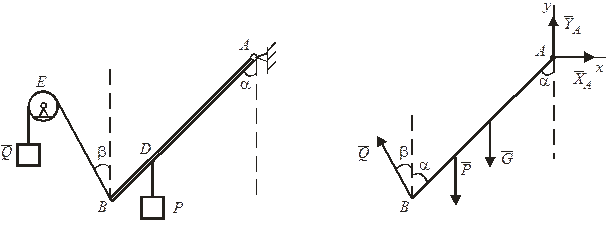
а) б)
Рисунок 2.6
Действие неподвижного шарнира заменим двумя составляющими 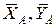 реакции и для уравновешенной произвольной плоской системы сил
реакции и для уравновешенной произвольной плоской системы сил 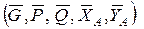 ~ 0 составим уравнения равновесия:
~ 0 составим уравнения равновесия:
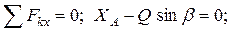
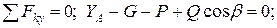
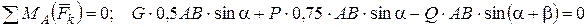 .
.
Решая эту систему уравнений, найдем из третьего уравнения системы:
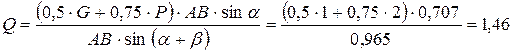 (кН).
(кН).
Из первого уравнения системы найдем:
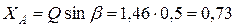 (кН).
(кН).
Из второго уравнения системы имеем:
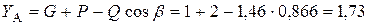 (кН).
(кН).
Пример 2.2
Определить реакции жестко закрепленной Т-образной балки, изображенной на рис.2.7,а, которая находится в равновесии под действием равномерно распределенной нагрузки интенсивности q=5 кН/м, сосредоточенной силы F=10 кH, наклоненной под углом 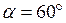 к вертикали, и пары сил с моментом
к вертикали, и пары сил с моментом 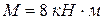 .
.
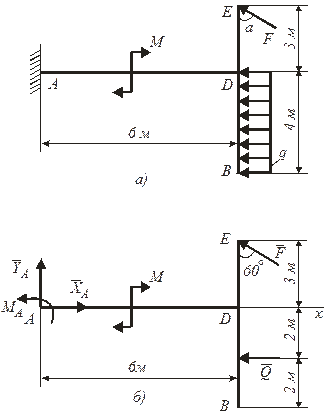
Рисунок 2.7
Решение
Рассмотрим равновесие консольной Т-образной балки 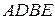 . Равномерно распределенную нагрузку заменим сосредоточенной силой
. Равномерно распределенную нагрузку заменим сосредоточенной силой 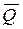 , которую приложим посредине участка BD, направив ее параллельно силам распределенной нагрузки в том же направлении. Вычислим, что
, которую приложим посредине участка BD, направив ее параллельно силам распределенной нагрузки в том же направлении. Вычислим, что 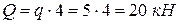 . Действие жесткого защемления на балку заменим двумя силовыми реакциями
. Действие жесткого защемления на балку заменим двумя силовыми реакциями 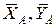 и реактивной парой сил с моментом
и реактивной парой сил с моментом 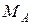 (рис. 2.7, б). Составим уравнение равновесия произвольной плоской системы сил, действующих на балку:
(рис. 2.7, б). Составим уравнение равновесия произвольной плоской системы сил, действующих на балку:
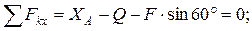
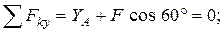
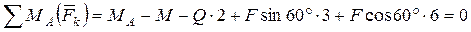 .
.
Решая эту систему уравнений, находим:
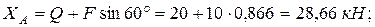
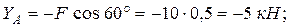
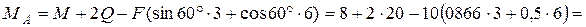
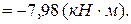
Дата добавления: 2015-09-14; просмотров: 1026;
