Методика и примеры решения задач. Рассмотрим примеры решения задач равновесия системы тел с применением указанных способов.

.

Рассмотрим примеры решения задач равновесия системы тел с применением указанных способов.

Пример 3.1

Найти реакции опор и давление в промежуточном шарнире С заданной на рис. 3.2 конструкции, которая состоит из невесомых угольника АС и стержня СВ. На конструкцию действуют пар сил с моментом М=50 кН, распределена нагрузка с интенсивностью q=10 кН/м, силы 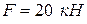и . И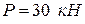звестны размеры .

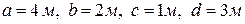Решение

При рассмотрении равновесия всей конструкции, как абсолютно твердого тела, три уравнения равновесия произвольной плоской системы сил, которые действуют на систему тел, будут содержать четыре неизвестные реакции: 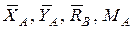(см. рис. 3.2, а).

Для устранения статической неопределенности разделим систему в точке соединения С и рассмотрим равновесие каждой части конструкции отдельно.

Сначала рассмотрим в состоянии равновесия стержень ВС, так как на него кроме известной активной силы, действует три неизвестные реакции 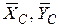шарнира С и 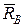гладкой поверхности в точке В (см. рис. 3.2, б), то есть задача равновесия стержня является статически определенной.

Составим три уравнения равновесия действующей на стержень произвольной плоской системы сил, воспользовавшись основной формой условий равновесия:

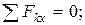
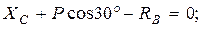
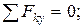
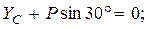
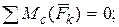
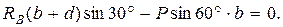
Составляя последнее уравнение, воспользуемся при нахождении 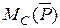теоремой Вариньона о моменте равнодействующей. Для этого разложим силу 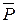на составляющие, одна из которых 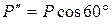параллельна стержню, то есть линия ее действия проходит через точку С и ее момент 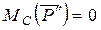, а другая 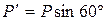перпендикулярная к стержню и имеет плечо относительно точки С, равное расстоянию b; ее момент .

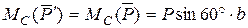Рассмотрим теперь равновесие угольника (рис. 3.2, в), к которому кроме активных сил приложим реакции 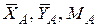жесткого защемления в точке А, и реакции 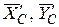шарнира С, направив последние противоположно реакциям 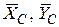балки ВС. Действие распределенной нагрузки заменим сосредоточенной силой 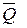( 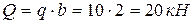), приложив ее посредине участка действия нагрузки. Для плоской системы, которая действует на угольник, также составим три уравнения равновесия:

;

;

.

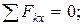
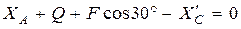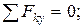
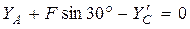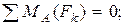
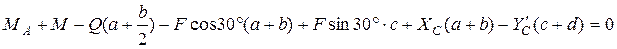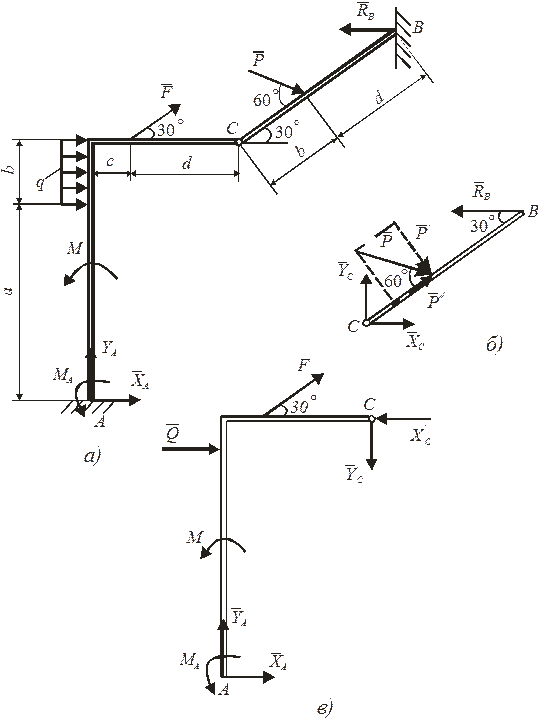
Рисунок 3.2

Учитывая, что 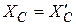и 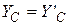, как силы взаимодействия, установим, что системы шести составленных уравнений содержат шесть неизвестных реакций, то есть задача статически определена.

Решая систему этих уравнений, найдем из третьего уравнения:

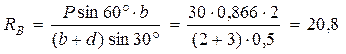(кН).

Теперь из первого и второго уравнения имеем:

;

.

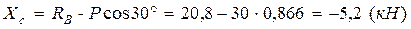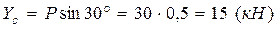Решаем уравнение системы равновесия угольника, подставляя туда вместо 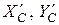значения 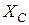и 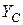с полученными знаками:

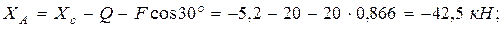
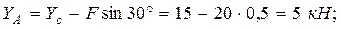
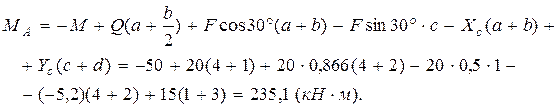
В соответствии со знаками реакций устанавливаем, что реакци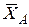и и 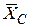направленные противоположно изображенным на расчетных схемах направлениям.

С целью проверки правильности решения составим и развяжем одно из уравнений равновесия системы сил, действующих на всю конструкцию:

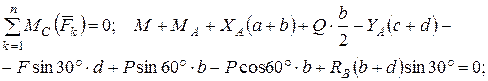
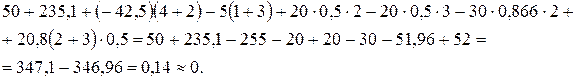
Следовательно, расчеты выполнены правильно.

Пример 3.2

На гладкой и блестящей горизонтальной поверхности стоит передвижная лестница, которая состоит из двух частей АВ и ВС, длиной 3м и весом Р = 120 Н каждая, соединенных шарниром С и веревкой ЕF так, что расстояние BF = АЕ = 1м. Центр веса каждой из частей АС, ВС находится в ее середине. В точке D на расстоянии CD = 0,6м стоит человек весом 720 Н. Определить реакции пола и шарнира и натяжение Т веревки EF, если угол ВАС = АВС = 45º.

Решение

Рассматривая лестницу как одно твердое тело (рис. 3.3,а), установим, что эта конструкция находится в состоянии равновесия под действием активных сил 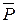веса каждой из частей лестницы и 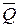веса человека, и реакций 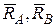гладкой и блестящей поверхности пола.

Эти силы составляют плоскую систему параллельных сил, для какого условия равновесия содержат два уравнения. Так, как в эту систему сил входит две неизвестные реакции, то задача равновесия лестницы является статически определенной. Составим уравнение равновесия этих сил:

.

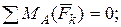
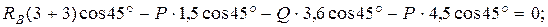
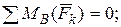
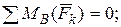
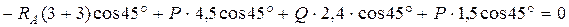Из этих уравнений находим:

.

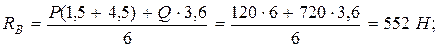
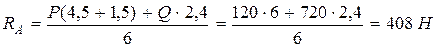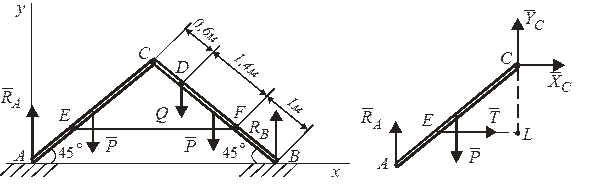
а) б)

Рисунок 3.3

Теперь рассмотрим равновесие части АС лестницы (рис. 3.3,б), на которую кроме активной силы 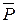веса действуют реакции 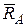гладкой и блестящей поверхности, 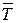веревки, 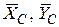шарнира. Для произвольной плоской системы сил составим уравнение равновесия:

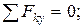
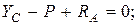
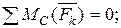
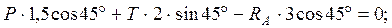
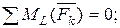
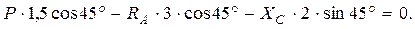
Здесь применена вторая форма уравнений равновесия произвольной плоской системы сил, которая обеспечивает упрощение их решения, так как в каждом из уравнений, входит лишь одна неизвестная величина.

Определим неизвестные реакции, учитывая, что sin45º = cos45º = 0,707.

.

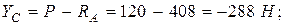
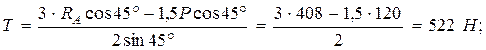
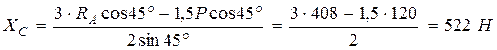Выполним проверку, убедившись, что выполняется уравнение равновесия для сил, прилагаемых ко всей конструкции:

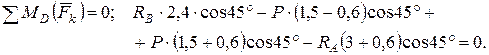
Отсюда, с учетом того, что, вычисляем:

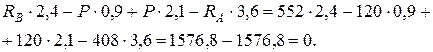
Следовательно, расчеты выполнены правильно.

Раздел 1 КИНЕМАТИКА