Рівновага утворення комплексів молекул у розчині

Перш ніж перейти до розгляду типів взаємодій між атомамий молекулами, розглянемо ще один приклад рівноваги у простій, але важливій для молекулярної біології системі.

У розчині певного об’єму містяться молекули двох типів (А і В), які здатні утворити між собою комплекс С (рис. 2):

(літерою K тут знову позначено константу рівноваги, у цьому випадку – для процесу утворення / дисоціації комплексів). Ентропійна частина вільної енергії кожного компонента містить складову, яка залежить від концентрації. Наприклад, вільну енергію G_A компонента А (що її в цьому випадку називають також хімічним потенціалом) можна записати як

де 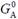– стандартна вільна енергія; R – універсальна газова стала, яка є константою Больцмана в перерахунку на моль речовини: R = k_BTN_AV, N_AV – число Авогадро (Amedeo Avogadro); квадратними дужками позначено молярну концентрацію А. Зміст рівняння (1.4) дуже простий: 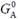є вільною енергією компонента А при його концентрації 1 моль/л; зростання концентрації призводить до зниження ентропії (чим більше молекул, тим менше доступних місць розташування для кожної з них, тобто тим меншим є кількість мікростанів, див. наведене вище визначення ентропії) і, відповідно, – до зростання вільної енергії.

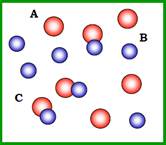
Рис. 2. Взаємодія між молекулами А і В з утворенням комплексу С.

Записавши аналогічні вирази для компонентів В і С, знайдемо різницю між правою та лівою частинами рівняння (1.3) ΔG = G_C – G_A – G_B:

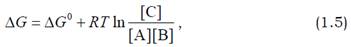
де ΔG⁰ – різниця між відповідними стандартними вільними енергіями, [A] і [B] – концентрації відповідних вільних компонентів у дисоційованому стані. Процес зміни концентрацій у системі буде продовжуватись до моменту досягнення рівноваги – такого співвідношення між концентраціями, коли вільна енергія комплексу дорівнюватиме сумарній енергії вільних компонентів А і В, і ΔG = 0. (Можна показати, що загальна вільна енергія розчину буде мінімальною, коли різниця ΔG між правою і лівою частинами рівняння (1.3) дорівнює нулю.).

Оскільки ΔG⁰ – це константа, яка залежить від природи компонентів, співвідношення концентрацій під логарифмом у рівнянні (1.5) також є константним за рівноважних умов. Саме це співвідношення і є в даному прикладі константою рівноваги, яка залежить тільки від різниці стандартних вільних енергій:

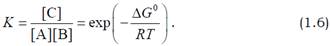
Отже, якщо при утворенні комплексу вільна енергія знижується(ΔG⁰ < 0), це сприяє взаємодії між компонентами. У випадку, що розглядається, константу K називають також константою асоціації, або константою зв’язування, а величину ΔG⁰ – стандартною вільною енергією зв’язування. Обидві константні величини є мірою спорідненості компонентів, що утворюють комплекс: чим негативнішою є енергія зв’язування (чим більше енергетично вигідних взаємодій реалізується між компонентами), тим вище значення K і тим стабільнішим є комплекс. Слід також зауважити, що ефективність утворення комплексу,під якою можна розуміти, наприклад, частку компонента А у складі комплексу – [C]/([C]+[A]), залежить від концентрації компонентів. Рівняння 1.6 є однією з форм запису відомого закону діючих мас, або принципу Ле Шательє (Henry Le Chatelier), згідно з яким додавання в систему одного з компонентів зсуває рівновагу в протилежний бік. Рівняння 1.3 може означати також рівняння хімічної реакції, коли внаслідок перебудови ковалентних зв’язків (див. нижче) у молекулах А і В, утворюється нова молекула С. Тоді рівняння (1.4) – (1.6) і висновки з них також зберігають свою силу. У цьому випадку також знак зміни стандартної вільної енергії вказує на напрямок, у якому відбувається хімічна реакція.

Варто підкреслити ще раз: усі хімічні реакції в живих системах відбуваються в напрямку зниження вільної енергії. Тут може виникнути запитання: якщо, наприклад, вільна енергія знижується при руйнуванні молекули С на А і В, але клітина має потребу саме в молекулі С, чи можливий синтез С? Відповідь є однозначною: синтез С із молекул А і В є неможливим. Але можна використати обхідний шлях: спочатку хімічно модифікувати одну з молекул (наприклад, утворити молекулу А′) і тоді може виявитися, що утворення С із А′ і В супроводжується зниженням вільної енергії, тобто є можливим.