Постановка задачи оптимизации ЭМ.
При оптимизации ЭМ нужно
1. Выделить независимые параметры
2. Выбрать целевую функцию
3. Выбрать метод оптимизацию
Независимые параметры в ЭМ бывают 2-х типов:
-дискретные (задаваемые технологическими и конструкторскими нормами)
-непрерывных
Обозначим вектор вирируемых параметров через 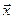 . На вектор параметров накладываются ограничения 2-х типов:
. На вектор параметров накладываются ограничения 2-х типов:
-прямые ограничения 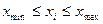 (1)
(1)
-функциональные  ,
, 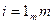 (2)
(2)
Функциональное ограничение выражают связи между параметрами ЭМ, в большинстве случаев они не линейны не выражаются аналитически, а заданы в виде цепочки формул позволяющих лишь вычислить их значения.
Выбор целевой функции представляет собой одну из основных трудностей, т.к. ЭМ представляет собой многокритериальную оптимизацию.
Выбор метода решения связан с видом целевой функции и видом ограничения. Если целевая функция позволяет провести исследования допустимой области и определить, что целевая функция унимодальная (имеет один экстремум), то целесообразно применение
траекторных методов и методов и методов типа спуска. Если такой информации нет, то применяют методы случайного поиска с различными модификациями.
Задачи оптимизации можно сформулировать следующим образом:
-найти оптимальный вариант
-найти такое сочетание варьируемых параметров которое доставляет max или min целевой функции, при этом выполняются ограничения 1-го и 2-го рода и вектор варьируемых параметров принадлежит допустимой области S.
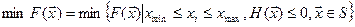
Дата добавления: 2015-09-11; просмотров: 1022;
