Постановка задачи оптимизации тягового двигателя

В электрической машине число переменных больше числа уравнений, которые их связывают. Поэтому при одних и тех же исходных данных можно получить большое количество вариантов расчёта. Но какой из этих вариантов будет лучшим (оптимальным)? Чтобы сделать такую оценку нужно выбрать функцию цели (критерий качества, критерий оптимальности). В электрической машине в качестве функции цели можно выбрать массу, КПД, стоимость и т.д. Но эти критерии носят противоречивый характер. Улучшение одного из них приводит к ухудшению другого. Оптимизация по какому-нибудь одному критерию называется оптимизацией по частному критерию (однокритериальная оптимизация). Оптимизация по одному критерию не позволяет получить электрическую машину с хорошими энергетическими и экономическими показателями. Оптимальным можно считать тот вариант расчета, у которого, например, масса и стоимость имеют близкие к минимально возможным значениям, а КПД - к максимально возможному значению. Оптимизация по нескольким критериям называется многокритериальной или векторной оптимизацией.

При оптимизации электрической машинынужно:

- выделить независимые параметры;

-выбрать целевую функцию;

-выбрать метод оптимизации.

Независимые параметры бывают 2- хтипов: дискретными (задаваемые технологическими и конструкторскими нормалями) и непрерывными. На вектор независимых параметров 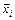накладываются ограничения 2-х типов: прямые ограничения (на диапазон их изменения) и функциональные ограничения (на величину численного значения функции, являющейся функцией варьируемых параметров).

Прямые ограничения имеют вид

, (1)

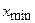где и 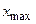минимальное и максимальное значение параметра.

Функциональные ограничения записываются в виде

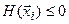, . (2)

Функциональное ограничение выражают связи между параметрами электрической машины, в большинстве случаев они не линейны и не имеют явной зависимости от варьируемых параметров.

Все известные методы многокритериальной оптимизации непосредственно или косвенно сводятся к задачам однокритериальной оптимизации. Иначе говоря, частные критерии тем или иным способом объединятся в составной критерий, который затем минимизируется или максимизируется.

Если оптимизация ведется без учёта статического разброса характеристик, то соответствующий критерий оптимальности называют детерминированным. Если разброс характеристик учитывается, то критерий статистический.

В задачах оптимизационного проектирования, в которых ищется экстремальное значение критерия без учёта ограничений на варьируемые параметры, называют задачами безусловной оптимизации. Найденные при этом экстремумы называют безусловными.

Наличие ограничений на варьируемые параметры приводит к задачам условной оптимизации, а экстремумы называются условными. Большинство разработанных методов оптимизации ориентировано на поиск безусловного экстремума. Задачи условной оптимизации приводят к задачам безусловной оптимизации или применяют специально разработанные методы.

Большинство задач параметрической оптимизации являются задачами нелинейного программирования, т.к. целевая функция и функциональные ограничения являются нелинейными функциями от вирируемых параметров. Если целевая функция и ограничения линейного зависят от вирируемых параметров, то такие задачи называются линейного программирования. Нелинейное программирование - это численные методы оптимизации.

Задача оптимизации электрической машины являются задачей нелинейного программирования.

Трудности оптимизации ещё заключаются и в том, что мы не имеем явной аналитической зависимости функции цели от варьируемых параметров. Математическая модель электрической машины представляет собой цепочку формул.

Выбор целевой функции представляет собой одну из основных трудностей, т.к. электрическая машина представляет собой задачу многокритериальной оптимизации.

Задачу оптимизации можно сформулировать следующим образом:

-найти такое сочетание варьируемых параметров которое доставляет max или min целевой функции, при этом выполняются ограничения 1-го и 2-го рода и вектор варьируемых параметров принадлежит допустимой области S, т. е.

.

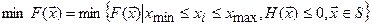Использование при оптимизации тяговых двигателей агрегированных (комплексных) переменных позволило ввести комплексный критерий

,

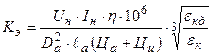где U_н - номинальное напряжение, В;

I_н - номинальный ток, А;

h - коэффициент полезного действия;

D_a - диаметр сердечника якоря, мм;

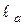- длина сердечника якоря, мм;

Ц_a - стоимость активных материалов двигателя, руб;

Ц_и - стоимость изоляционных материалов двигателя, руб;

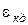- допустимое значение критерия коммутационной напряженности;

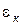- текущее значение критерия коммутационной напряженности. Критерий коммутационной напряженности 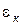учитывает качество коммутации и потенциальные условия на коллекторе.

Максимум введенного критерия K_э­ хорошо согласуется с экстремальными значениями частных критериев. Это означает, что из возможного множества решений получено такое сочетание параметров, при котором активная мощность, приходящаяся на единицу объема и на рубль затрат, имеет максимальное значение при минимально возможном критерии коммутационной напряженности.

Критерий K_э­ является функцией варьируемых переменных 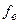, , 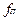, , 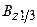, 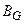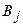. Аналитические исследования позволили установить, что критерий K_э­ является унимодальной (одноэкстремальной ) функцией варьируемых параметров, причем максимум этого критерия находится в узком вычисленном диапазоне параметров 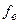и 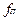. Увеличение индукции в зубцах якоря 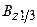и в зубцах компенсационной обмотки до технически обоснованных пределов, приводит к возрастанию K_э­ . Это позволяет перевести их в вектор фиксированных переменных. Индукции в главном полюсе B_G и в остове B_j не влияют на качество якоря, а на качество всего двигателя их влияние проявляется в величине стоимости активных и изоляционных материалов и коэффициента полезного действия. В связи с этим для статора целесообразно ввести отдельный критерий

,

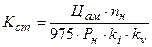где Ц_ам - стоимость активных материалов статора, руб;

n_н - номинальная частота вращения, об/мин;

P_n - номинальная мощность, кВт;

k_i - коэффициент использования мощности;

k_v - коэффициент регулирования скорости.

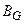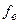Критерий K_cm хорошо согласуется с критерием K_э­ . Минимальное значение критерия K_cm доставляет максимум критерию K_э­ . Введение этого критерия для статора позволяет более точно учесть влияние индукций , на его оптимальное состояние, а также рассматривать критерием K_э­ в явном виде как функцию двух переменных и .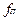

Учитывая, что диапазон изменения 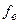и 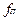, в котором критерий достигает максимального значения известен, а также считая диаметр якоря D , число пазов на пару полюсов Z 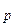и число пар полюсов заданными, можно вычислить диапазон изменения высоты и ширины проводника обмотки якоря.

Выбор метода оптимизации связан с видом целевой функции и видом ограничений. Если целевая функция позволяет провести исследования допустимой области и определить, что целевая функция унимодальная (имеет один экстремум), то целесообразно применение

траекторных методов и методов и методов типа спуска. Если такой информации нет, то применяют методы случайного поиска с различными модификациями.

Оптимизация тягового двигателя производится методом рационализированного перебора. Сущность этого метода заключается в том, что для сокращения объема вычислений на ранней стадии расчета вводится ряд проверок технической пригодности оптимального варианта (по допустимому расстоянию между катушками полюсов, по допустимой ширине ножки зубца якоря и другие).

Блок-схема программы оптимизации тягового двигателя приведена

на рис.1.

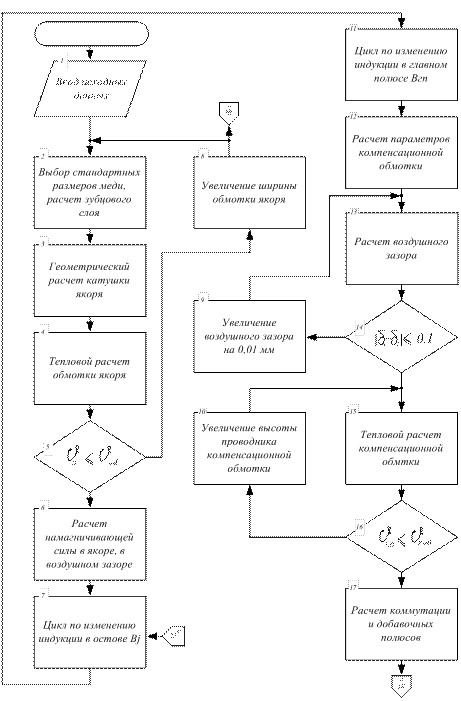
Рис.1. Лист 1. Блок-схема программы оптимизации тягового двигателя

Рис.1. Лист 2. Блок-схема программы оптимизации тягового двигателя