Постановка задачи расчёта двухмерного температурного поля.

Температурное поле в общем случае в двухмерной области описывается нелинейным дифференциальным уравнением частных производных вида:

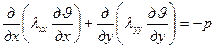(2)

Где 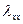, 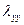-коэффициенты теплопроводности по осям x и y

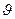-температура (превышение температуры)

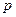-мощность тепловыделений (потери)

Уравнению (2) могут соответствовать 2 вида граничных условий: условие Дирихле, т.е. когда задана температура на границе 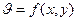или условие Коши, т.е.

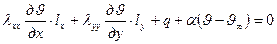
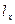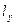, -направляющие косинусы внешней нормали к граничной поверхности.

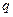-поток тепла через единичную поверхность.

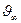-превышение температуры охлаждающей среды.

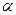-коэффициент теплоотдачи.

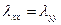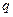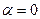Если ; и , то

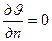
Сравнивая уравнения (1) и (2) видим, что они имеют один и тот же вид. Это позволяет использовать 1 алгоритм формирования расчётной системы уравнения.

Рассмотрим расчётную область, в которой будем находить решение поставленной задачи. Область представляет собой сектор машины постоянный ток якоря, приходящийся на половину полюсного деления. Расчёт ведётся без учёта реакции якоря (машина с компенсационной обмоткой и действие реакции якоря незначительное).

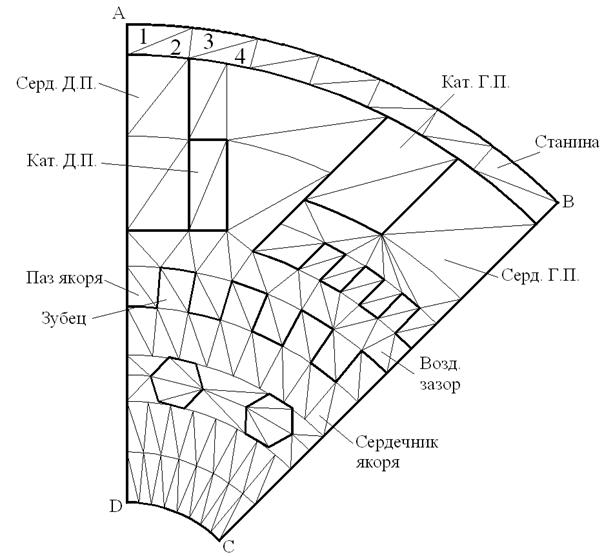
Расчёт магнитного поля производится для всех элементов области (в стали и в воздухе).

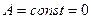
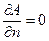
Для температурного поля область остаётся той же, но количество узлов и количество треугольников изменяется, исключаются узлы и треугольники, легко делящиеся в воздухе.

В тепловой задаче граничные условия выглядят следующим образом AD, DC, BC 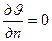, а на всех остальных границах, омываемых воздухом выполняется условие Коши.