Классификация М.М.

По характеру отображаемых свойств М.М. делится на структурные и функциональные.

Структурные предназначены для отображения структурных свойств объекта.

Различают топологические и геометрические М.М. В топологических М.М. отображаются состав и взаимосвязь элементов объекта они могут иметь форму матриц, таблиц и списков.

В геометрической М.М. отображается геометрические свойства объекта в них дополнительно а сведениям о взаимном расположении объектов содержащих сведения о форме детали (они выражаются совокупностями уравнений и алгебраическим соотношением и т.д.).

Функциональные М.М. предназначены для отображения физических и информационных процессов протекающих в объекте. Обычно функциональные М.М. представляют собой системы уравнений связывающие внешние и внутренние выходные параметры. Функциональные М.М. могут описывать электромеханические, механические, гидравлические, оптические, химические и др. процессы функционирования объектов.

М.М. комплексного расчёта магнитных и температурных полей (пример М.М. на микроуровне. Для расчёта температурных полей необходимо знать распределение источников тепловыделений, это в первую очередь относится к областям с ферромагнитными материалами т.к. распределение индукции в магнитопроводе электрической машины то и неравномерно распределены источники тепловыделения (Р_ст).

Потери в элементах магнитопровода состоят из двух составляющих: потери на гистерезисе и от вихревых токов. Для их расчёта необходимо знать индукции отдельных элементов. Для расчёта распределения индукции необходимо рассчитать магнитное поле. Для облегчения

расчёта магнитного поля с токонесущими областями используют векторный магнитный потенциал.

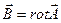
Магнитное поле (2^х мерное) в неоднородной нелинейной среде описывается нелинейным дифференциальным уравнением в частных производных.

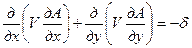(1)

Где А и 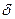-составляющие векторы магнитного потенциала и плотности тока по оси Z.

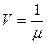-нелинейная величина.

Уравнение (1) получено при следующих допущениях:

-ферромагнитные материалы магнитопровода изотропии и явление гистерезиса не учитываются.

-не учитывается действие вихревых токов.

-заданные токи равномерно распределены по токонесущим областям и изоляцией этих областей, можно пренебречь.

Уравнению (1) могут соответствовать различные граничные условия, можно выделять 3 граничных условий:

1. расчёт магнитного поля при ХХ

2. расчёт магнитного поля в отдельных областях поперечного сечения машины

3. расчет магнитного поля при нагрузке.

В 1^х 2^х типах задач заданы условия Дирихле, т.е. на границах области (отдельных областях) заданы значения векторного потенциала, а на других участках заданы условия Неймана.

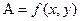(Дирихле)

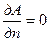(Неймана)

В 3^м типе задач, если нагрузки симметричный векторный магнитный потенциал является функцией двойного полюсного деления. Это позволяет выбрать граничные условия так, чтобы рассчитать магнитное поле только на одном полюсном делении (условия периодичности).

В областях с разными средами (воздух-сталь) должны выполнятся следующие условия на границе раздела; т.е. должны быть равны нормальные значения индукции и касательные составляющие напряженности магнитного поля.

B_n и H_t

В методе конечных элементов эти условия выполняются автоматически при получении расчётных уравнений.

В методе конечных элементов (МКЭ) энергетичный функционал, соответствующий уравнению (1) (для 2^х мерного поля) заменяется системой нелинейных алгебраических уравнений.

Для получения расчётной системы нелинейных уравнений расчётная область разбивается на большое количество подобластей (элементов), они могут быть прямоугольные, треугольные и т.д. Наиболее проста система расчётных уравнений получается для треугольных элементов, с их помощью легко апроксимируется сложная граница области.

Для формирования системы расчётных уравнений необходима следующая информация:

1. количество расчётных узлов внутри области

2. количество треугольных элементов

3. массив номеров треугольников и номеров вершин, которые образуют этот треугольник

4. координаты всех узлов области (x,y)

5. массив номеров треугольников с указанием признака среды, где расположен треугольник (воздух или железо).