Приближения формулы Бернулли
При больших значениях n подсчет вероятностей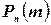 
по формуле (2.4) связан с громоздкими вычислениями. В этом случае удобнее пользоваться приближенными формулами.
1. Локальная формула Муавра-Лапласа.
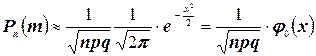(2.6)
где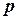 
не равно нулю и единице, 
, а
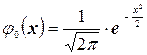. (2.7)
Формула (2.6) выражает так называемую локальную теорему Лапласа (П. Лаплас (1749—1827) — французский математик и астроном.). Точность этой формулы повышается с возрастанием n.
Функция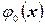 
формула (2.7), как мы увидим в дальнейшем, играет очень большую роль в теории вероятностей (см. рис. 2.1). Ее значения при различных значениях аргумента приведены в Приложении (см. табл. I). Она представляет собой функцию вероятности нормального распределения (мы еще вернемся к ней). При 
, 
, поэтому функция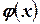 
затабулирована для 
.
Пример 11. Игральную кость бросают 80 раз. Определить вероятность того, что цифра 3 появится 20 раз.
Решение: Здесь m=20; n=80; p=1/6; q=1-1/6=5/6; далее находим
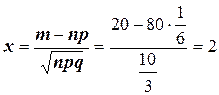
Используя формулу (15), получим
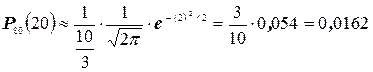
так как из табл. I находим, что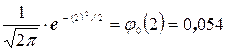 
.
2. Если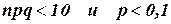 
то используют так называемую формулу Пуассона
(2.8)
Пример 12.Завод отправил 5000 доброкачественных изделий. Вероятность того, что в пути разбили одно изделие - 0,0002. Найти вероятность того, что в пути будет повреждено:
а) 3 изделия;
б) 1 изделие;
в) не более трех изделий.
Решение. Имеем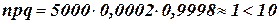 
и 
, поэтому применяем формулу Пуассона.
а) 
: 
.
б)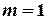 
: 
.
в) 
:
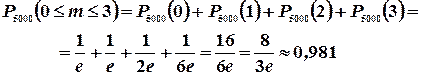
3. При больших значениях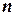 
, для вычисления вероятности того, что произойдет от 
до 
событий по схеме Бернулли, используется интегральная формула Муавра-Лапласа:
где 
,
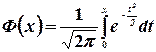(2.9)
- функция Лапласа (см. рис. 2.2.).
К функции Лапласа мы еще не раз будем обращаться, а пока отметим, что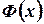 
имеет следующие свойства.
1) 
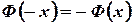- функция нечетная, поэтому достаточно применять ее для неотрицательных значений 
;
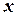2) функция 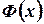возрастает на всей числовой оси;
3) при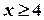 
, 
( 
- горизонтальная асимптота при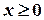 
), поэтому функция представлена в виде таблицы для 
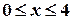(Прил. I);
4) вероятность отклонения относительной частоты 
от постоянной вероятности 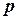в независимых испытаниях не более чем на некоторое число 
равна:
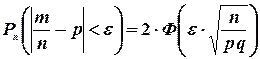
Пример 13. Стрелок выполнил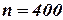 
выстрелов, вероятность одного попадания 
. Найти вероятность того, что он попадет от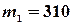 
до 
раз.
Решение. Согласно интегральной формуле
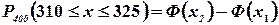, где
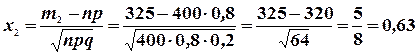
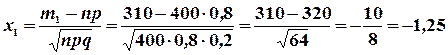
Пример 14. В каждом из 
независимых испытаний вероятность успеха 
. Найти вероятность того, что относительная частота появления события отклонится от постоянной вероятности по абсолютной величине не более чем на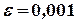 
.
Решение.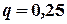 
, следовательно
Пример 15. Сколько раз нужно бросить монету, чтобы с вероятностью 
можно было ожидать, что отклонение относительной частоты появления герба от вероятности 
окажется по абсолютной величине не больше чем на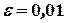 
?
Решение. По условию 
. Отсюда
.
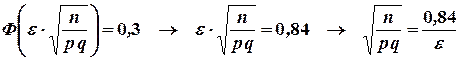
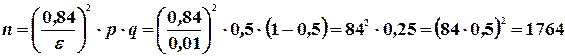Дата добавления: 2015-09-11; просмотров: 1358;