Вероятность появления хотя бы одного события.

ПОСЛЕДОВАТЕЛЬНЫЕ ИСПЫТАНИЯ.

Оглавление.

1. Вероятность появления хотя бы одного события.

2. Формула Бернулли.

3. Приближения формулы Бернулли.

Вероятность появления хотя бы одного события.

Пусть в результате испытания могут появиться псобытий, независимых в совокупности, либо некоторые из них (в, частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Чтобы найти вероятность того, что наступит хотя бы одно из этих событий, воспользуемся следующей теоремой.

Теорема 4: вероятность появления хотя бы одного из событий 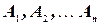, независимых в совокупности, равна разности между единицей и произведением вероят­ностей противоположных событий :

.

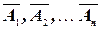Доказательство: обозначим через Асобытие, состоящее в появлении хотя бы одного из событий 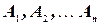. События Аи 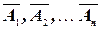(ни одно из событий не наступило) противоположны, следовательно, сумма их вероятностей равна единице:

.

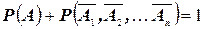Отсюда, пользуясь теоремой умножения, получим

,

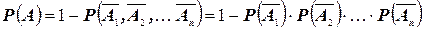или

. (2.1)

Частный случай: если события 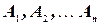имеют одинаковую вероятность, равную р, то вероят­ность появления хотя бы одного из этих событий равна

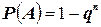. (2.2)