Формула Бернулли. Предположим теперь, что производится n независимых испытаний в неизменных условиях, в результате каждого из которых может наступить или не наступить некоторое

Предположим теперь, что производится n независимых испытаний в неизменных условиях, в результате каждого из которых может наступить или не наступить некоторое событие A. Пусть при каждом испытании вероятность наступления события А одинакова и равна . Следовательно, вероятность противоположного события (ненаступления А) равна .

Определим вероятность 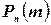того, что событие А произойдет m раз при этих n испытаниях.

При этом заметим, что наступления или ненаступления события А могут чередоваться различным образом. Условимся записывать возможные результаты испытаний в виде комбинаций букв и . Например, запись означает, что в четырех испытаниях событие осуществилось в 1-м и 4-м случаях и не осуществилось во 2-м и 3-м случаях.

Всякую комбинацию, в которую входит 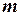раз и, соответственно, входит раз, назовем благоприятной. Количество благоприятных комбинаций равно количеству способов, которыми можно выбрать 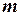чисел из данных 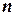; таким образом, оно равно числу сочетаний из nэлементов по m, т.е.

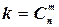
Подсчитаем теперь вероятности благоприятных комбинаций. Рассмотрим сначала случай, когда событие A происходит в первых 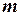испытаниях и, следовательно, не происходит в остальных испытаниях. Такая благоприятная комбинация имеет следующий вид:

Вероятность этой комбинации в силу независимости испытаний (на основании теоремы умножения вероятностей) составляет

Так как в любой другой благоприятной комбинации событие встречается также 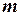раз, а событие происходит раз, то вероятность каждой из таких комбинаций также равна 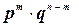. Итак

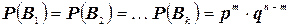
Все благоприятные комбинации являются, очевидно, несовместными. Поэтому (на основании аксиомы сложения вероятностей)

Следовательно,

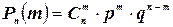(2.3)

Или, так как 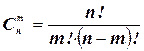, то

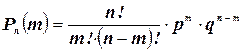(2.4)

Формула (2.4) называется формулой Бернулли (Я. Бернулли (1654-1705) - швейцарский математик).

Так как вероятности 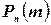для различных значений 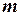представляют собой слагаемые в разложении бинома Ньютона:

то распределение вероятностей 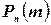, где , называется биноминальным.

Пример 9. Вероятность попадания в цель при одном выстреле равна 0,6. Какова вероятность того, что 8выстрелов дадут 5 попаданий?

Решение: Здесь n = 8; m = 5; p = 0,6; q = 1- 0,6 = 0,4.

Используя формулу (2.4), имеем

Часто необходимо знать, при каком значении 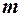вероятность принимает наибольшее значение, т. е. требуется найти наивероятнейшее число наступления события Aв данной серии опытов. Можно доказать, что число 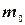должно удовлетворять двойному неравенству

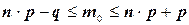(2.5)

Заметим, что сегмент 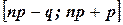, в котором лежит 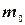, имеет длину 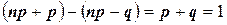. Поэтому, если какой-либо из его концов не является целым числом, то между этими концами лежит единственное целое число, и 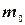определено однозначно. В том случае, если оба конца — целые числа, имеются два наивероятнейших значения: 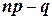и .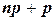

Пример 10. Определить наивероятнейшее число попаданий в цель в примере 1.

Решение: Здесь ; ; ; ; .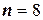

Согласно формуле (2.5) наивероятнейшее значение 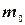лежит на сегменте 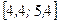и, следовательно, равно 5.