Есептеу тәсілдері» мазмұндық-әдістемелік желі материалдарын оқыту технологиясы.

1.«Есептеу тәсілдері» мазмұндық-әдістемелік желі материалдарын оқыту технологиясы.

2.Желінің негізгі нысандары: «ерекше» (нөл және бірмен байланысты).Желінің негізгі нысандары:кестелік және кестеден тыс жағдайлардағы ауызша есептеу тәсілдері; арифметикалық амалдар алгоритмі.

3.Сандарға амалдар қолдану тәсілдерін кезеңдер бойынша оқыту және есептеулер орындау құзыреттіліктерін қалыптастыру технологиясы.

1. Математиканы оқытудың негізгі мақсаттарының бірі-бастауыш сыныпта мұғалімнен балаларда ауызша және жазбаша есептеулердің берік дағдысын қалыптастыру, оқушыларды натурал сандар мен амалдар орындай білуге және сол амалдарды қарапайым шамаларға қолдануға үйрету. Оқушылардың бастауыш буынды бітіруіне қарай бірдей дәрежедегі математикалық дайындықтан өтуін қамтамасыз ететін есептеулер жүргізу іскерліктері мен дағдыларының минимум деңгейі бағдарламада анықталған.

Есептеулер жүргізу дегеніміз – оқып үйренген нысандар мен ауызша немесе жазбаша амалдар орындау. Ауызша есептеулерде қосу (азайту) мен көбейту (бөлу) кестелері, амалдардың «ерекше» және кестеден тыс жағдайлары жайындағы білімдер, ал жазбаша орындалғанда амал алгаритомдері қолданылады. Бұлардың бәрі–есептеуге машықтандырудың құрамды бөліктері. Есептеудің орындалу сапасы оқыту нәтежелерінің нақты деңгейіне байланысты. Оны бағдарлама талаптарына сай қалыптастыру үшін мыналар қажет:

1) әр түрлі көрнекі құралдарды тиімді пайдалану және есептеулер жүргізу теориясы мен практикасының ара қатынасын дұрыс сақтау арқылы олардың қатесіз орындалуына негіз жасау;

2) есептеулер саналы және дұрыс жүргізіліп қана қоймай, оны сенімді де шапшаң орындау дағдыларын орнықтыра, жетілдіре түсетін жұмыстарды дәйекті және жүйелі, әрі уақыт жағынан үйлесімді ұйымдастыру;

3) бүкіл сыныптың және жекелеген оқушының есептеулер жүргізуге бейімділігін әрдайым тексеріп, анықталған кемшілік пен ол қылықтардың дер кезінде жойылуына үнемі қамқорлық жасап отыру. (әр оқушының өзіне тән жеке ерекшеліктерді де айрықша ескерту);

4) есептеулер жүргізуге үйретудің қай кезеңінде болмасын, оқушының өзін-өзі тексеру мен бақылауына басшылық ету.

Математика теоремасын оқып үйренгенде кейбір дәлелдеулерді логикалық түрде байымдау білуді талап етумен қатар, осы дәлелдеулерді ауызша есептеу әдістерін негіздеу үшін пайдалана білуді талап етеді. Бастауыш сынып оқушылары ауызша есептеу әдістерінің барлығын да арифметикалық амалдардың заңдарымен, қасиеттерімен негіздей алуы керек.

Есептеу қабілетін қалыптастыру, жетілдіру және дамыта түсумен байланысты қазіргі әдістеменің принциптік және мәнді белгілері болып табылатын бұл талаптар математиканы оқыту мазмұнын анықтауда маңызды роль атқарады. Өйткені, оқытылатын материалдар осы тұрғыдан іріктеліп алынады, олардың құрылымы мен қарастылу кезеңдері анықталады, ауызша және жазбаша есептеу тәсілдерінің белгілі бір ара қатынасы тағайындылады. Жалпы алғанда, ауызша және жазбаша есептеу тәсілдерінің түрлерін іріктеп алу өте оңай шешілетін мәселе емес, өйткені қай тәсілдің басымырақ болуын ғылыми - техникалық жетістіктер мен өмір талабы анықтайды.

Мысалы, қазіргі кезде жоғарғы сыныпта микрокалькуляторлармен жұмыс жасауға оқушыларды үйрету есептеулерді қатесіз, шапшаң жүргізуде барынша тиімді екенін тәжірибе көрсетіп отыр. Қарапайым микрокалькуляторларды бастауыш буында да қолдану мүмкіндігі ғылыми зерттеулер мен озық тәжірибелер нәтижесінде дәлелденіп, оның тиімділігі анықталған уақытта ауызша және жазбаша есептеу тәсілдерінің қазіргі арақатынасы белгілі бір өзгерістерге ұшырауы ықтимал.

Жалпы алғанда, ауызша және жазбаша есептеу тәсілдерінің түрлерін іріктеп алу өте оңай шешілетін мәселе емес. Өйткені қай тәсілдің басымырақ болуын ғылыми-техникалық жетістіктер мен өмір талабы анықтайды. Шараушылықтың әр түрлі салаларына электрондық есептегіш машиналардың батыл енгізілуі ұзақ жылдар бойы практикада қалыптасқан ауызша және жазбаша есептеулер жүргізу тәсілдерінің арақатынасын түбегейлі қайта қарауды талап етеді. Төрт жылдық бастауыш мектептің алғашқы екі класында есептеудің ауызша тәсілдері басымырақ та, арифметикалық амалдар көбінесе үшінші, төртінші ғана жазбаша орындалады, яғни амал алгоритмдерін жүйелі оқып үйрену бір ғана кластың үлгісіне тиеді. Бұл - оқушыларға артық жүктеме туғызып, қиындық келтіреді. Төрт жылдық бастауыш мектепте ауызша және жазбаша есептеулер жүргізудің арақатынасын жаңаша жолға қою талабының тағы бір себебі осыдан деп білуіміз керек. Мұның өзі ұзақ жылдар бойы бастауыш буын математикасын оқыту процесін бақылау мен арнайы зерттеулер қорытынды-сында негізделген. Ал, бұл – есептеу бейімділігі мен оған машықтану деңгейін жоғары сатыға көтеруге мүмкіндік беретін озық тәжірибе нәтижелері дәлелдейді.

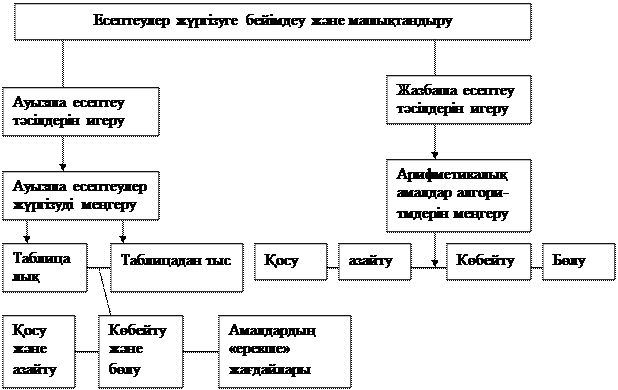Бағдарлама мен оқулықтар көздеп отырғандай, математиканы оқыту процесінде қалыптасатын есептеуге бейімділік пен оған машықтанудың өзара байланысын төмендегідей шартты блок-схема түрінде көрсетуге болады.

Осы схемадағы талаптар жүйесі есептеулер жүргізудің сапасын анықтайды.

2. Есептеулер жүргізуде арифметикалық амалдарды орындаудың «ерекше және дербес» жағдайлары жиі кездеседі. Олар арифметикалық амалдарды орындағанда 0 мен 1 сандары қатысатын жағдайлар. Бұлар тірек білімнің қатарына жатады, себебі, сандармен ауызша және жазбаша есептеулер жүргізудің барсыныда оқушылардың қатесіз және автоматты түрде осындай жағдайларды қарастыруына тура ке-леді.

Демек, арифметикалық амалдардың «ерекше және дербес» жағдайларын алдымен оқушылар саналы түсінуі тиіс те күнделікті сабақтар әр алуан жаттығулар орындау барысында автоматты дәрежеде орныдау деңгейіне жеткізілген сәйкес-дағдыларды қалыптастыру үшін жүйелі жұмыс жүргізу әрдайым мұғалімнің назарында болуы керек.

Мұндағы ең басты мәселе осындай жағдайларды салыстыра қарастыру барысында оқытылып отырған мәселені оқушылардың саналы игеруіне жету және ары қарай жұмыс барысында ондай жағ-дайларды салыстыра қарастыру арқылы әрқайсысының өзіне тән ерекшелігін, сондай-ақ олардың әр түрлі топтарының ұқсастығын та-ғайындау. Сонымен бірге ондай білімдерді саналы қабылдауын қамтамасыз ету. Бұл жағдайлар жеке дара қарастырылады. Сондық-тан амалдардың кестелік жағдайларының құрамына бұлар енгізіл-иейді. Ол қосу мен көбейту, азайту мен бөлудің сәйкес жағдайларына қатысты таблицаларды біршама ықшам түрде құруға мүмкіндік туғы-зып отыр. Сондай-ақ балалардың есте сақтауына тиісті кестелік жағдайлардың мөлшерін (санын) әлдеқайда кемітуге себепші болуда.

Алдымен оқушылардың танысатын мәселесі санға 1-ді қосу және саннан 1-ді алу. Бұл есептеу тәсілінің теориялық негізі натурал сандар қатарының негізгі қасиеті. Егер n кез келген натурал сан болса, онда алдыңғы n-1 саны шығады.

Әрине осы қасиеттің жалпы түріндегі тұжырымдамасын балалардың келтіруі және оны жан-жақты айтуы міндетті емес. Оны балалардан талап етуге болмайды. Осы жерде оны мұғалімдердің есіне салу үшін ғана келтіріліп отырғанын ескертеміз.

Дегенмен, ол тұжырымдама мен мән-мазмұнын оқушылар сезінуі тиіс және нақты мысалдарды қарастыру барысында біртіндеп қолдануға машықтануы керек. Сондықтан нақты мысалдар арқылы осы қасиеттің мән-мазмұнын аша түсуге 10 көлеміндегі сандардың нумерациясын оқып-үйрену кезінен – ақ ерекше көңіл бөлу қажет.

Осы тұрғыда заттардың не нәрселерді санау, яғни зат не нәрсе мен санды сәйкестендіру; санды 1-ге қосу және 1-ді азайту арқылы шығарып алу; сандар қатарын тура және кері ретпен атау; кез келген саннан бастап 1-ден қоса және 1-ден шегере санау; сандар қатарына бір санды атап отырып екі бағытта атау; қалдырып кеткен сандар қатарындағы санды т.с.с. жаттығуларды, сондай–ақ әр алуан көрнекі-ліктің түрлері мен дидактикалық материалды қажетінше және тиімді пайдалану керек болады .

Сонда ғана осы қасиетке негізделген есептеу тәсілінің мәнін оқушылар саналы қабылдайды және игереді .

Келесі қарастырылатын мәселе 0-ді қосу ,0-ді азайту ,0- ге санды қосу, азайтуда 0-дің шығатын жағдайлары, жалпы 0 саны ұғымын енгізу аса күрделі мәсел. Сәйкес түсініктің дұрыс және саналы игерілуі ілгерді азайтуды орындағанда 0-дің шығуы және 0-ге санды қосқан жағдайда нәтиженің сенімді табылуына негіз қалайды. Сондықтан әр түрлі көрнекілікті пайдаланып, ол мәселені оқушылардың берік игеруін қамтамасыз ету керек.

Бастауыш буында математика курсын оқытудың ең негізгі мақсаты – арифметикалық амалдардың кестелік жағдайларын оқушылардың саналы және берік игеруін қамтамасыз ету. Бір таңбалы сандарды қосу мен көбейту кестесін және азайту мен бөлудің сәйкес жағдайларын жатқа білу – осы талаптардың құрамдас бөлігі. Бұған жету үшін табилцаларды оқытып үйретудің негізгі ерекшеліктеріне сай қолайлы методикалық мүмкіндіктер творчестволықпен пайдаланылуы тиіс.

Жалпы алғанда арифметикалық амалдардың кестелік жағдайларын оқытуда, таблицаны оқушылардың табысты меңгеруін жеңілдету мақсатында барлық кестелік жағдайлар бірнеше топтарға бөлінгендігін ескерген жөн. Мұнда амалдарды орындату тәсілдері бірдей (ортақ) болатын кестелік жағдайлар жекелеген топтар құрайды. Оған қоса ілгеріде қарастырылатын топтың негізгі есептеу тәсілін үйрену, оның алдында оқып – үйренген кестелік нәтижелерді оқушылардың меңгеру сапасына тәуелді. Өйткені мұнда оқытудың алдынғы кезеңдігі нәтижелері тірек білім ретінде қолданылады.

Осыған орай қазірде арифметикалық амалдардың кестелік жағдайлары мынандай топтар құрады:

1. Бір таңбалы сандарға (10 көлеміндегі) 2,3,4 сандарын қосу мен азайтудың сәйкес жағдайлары;

2. Бір таңбалы сандарған (10 көлеміндегі) 5,6,7,8,9, сандарын қосу және азайтудың сәйкес жағдайлары;

3. 20-ның көлеміндегі қосу кестесі және азайтудың сәйкес жағдайлары;

4. 100-дің көлеміндегі көбейту кестесі және бөлудің сәйкес жағдайлары.

Мысалы, кестелік қосу мен азайтудың 2,3,4,5 сандары мен жағдайларын оқытып үйретудің әдістемесінде бірізділік сақталады. Мұндағы қосу тәсілі сан сызғыштан да 2,3,4,5 сан аттай отырып тура бағытта, ал азайту тәсілі сәйкес кері бағытта санау арқылы түсіндіріледі. Қосылғыштарының бірі 2,3,4,5 сандары болатын жағдайлардағы санның құрамын есте сақтауға баса көңіл бөлінеді және сәйкес азайтуды сол білімді қолдануға машықтандыру көзделеді.

Қорытынды нәтиже – қосу кестесінің 16 теңдігін жатқа білдіртіп шығару, яғни

2+2=4

3+2=5

4+2=6 3+3=6

5+2=7 4+3=7

6+2=8 5+3=8 4+4=8

7+2=9 6+3=9 5+4=9

8+2=10 7+3=10 6+4=10 5+5=10

3) □ ± 6,7,8,9 түріндегі азайту

Кестелік жағдайларды оқытудың келесі сатысында 6,7,8,9 сандарын қосу және азайту тәсілдері қарастырылады.

Бұл жағдайлардағы қосу – сандарының орындарын ауыстырып қосуға болатындығына сүйеніп, яғни қосу амалының ауыстырымдылық қасиетіне негізделіп, бұрыннан оқушылар назары үлкен санға кіші сан-ды қосудың қолайлы екеніне аударылады. Сондай-ақ, сәйкес санды азайту, қосу кестесіне сүйеніп, яғни санның құрамы жайындағы білім-нің негізінде орындалатыны арнайы аталып отырылады.

Қосуға берілген бір ғана мысалдың нәтижесін пайдаланып, тағы да 3 (қосуға -1, азайтуға -2) мысалдың нәтижесін табудың үлгісі көрсе-тіледі, бұған оқушылар мейлінше жаттығуы тиіс. Мысалы,

8+2, 2+8, 10-2, 10-8.

4) 10-□. Кестелік қосу мен аазйтуды оқытып-үйретудің соңына қарай 10 санынан азайту жағдайларына арнайы тоқталып өту көзделеді.

Тақырыпты оқып-үйренудің соңына қарай қосу кестесін еркін білу және азайтудың сәйкес жағдайларына нәтижені табу үшін қосу кестесі теңдіктерін қолдануға жетік машықтану жүзеге асырылуы тиіс.

3. “Қосу және азайту” тақырыбын оқып үйрену нәтижесінде оқушылар 100 көлеміндегі кез келген сандарды қосу мен азайтуды саналы түрде үйреніп, ондықтан аттап қосу мен азайтудың кестелік жағдайларын, сондай-ақ бірқатар теориялық мәселелерді берік игеріп алулары тиіс.

Бірінші ондықты оқып үйренгендегідей, 100 көлеміндегі қосу мен азайту әдістері теориялық материалды оқып үйренумен табиғи байланыста айқындалады. Мұндай әдісті қолданғанда теория мәселелері жақсы ұғынылады, өйткені олар қолданыс тауып, неғұрлым саналы ұғынылған есептеу дағдылары тезірек қалыптасады.

100 көлеміндегі сандарды қосу және азайту әдістерін талдау, оларды саналы түрде орындау үшін оқушылар 100 көлеміндегі сандардың нумерациясын жақсы біліп, 10 көлемінде қосу таблицасы мен азайтудың соған сәйкес жағдайларын берік білулері тиіс.

Жазбаша қосу мен азайтудың тәсілдерін оқыту әдістемесі төмендегіше:

Қосу мен азайтудың алгоритмдері екі таңбалы санды мысалға ала отырып енгізіледі. Қосу мен азайтудың жазбаша тәсілдерін ілгеріде сандар аймағының кеңеюіне алынған білімді тасымалдау жүзеге асырылады.

“Баған” түрінде қосу мен азайтудың жазбаша тәсілдерімен таныстыру (бір сабақта қатар).

Кестенің бірінші қатарындағы санды оқы. Ол

санның ондықтары мен бірліктерін қандай

цифрлар көрсетеді? Кестенің екінші қатарындағы

санды оқы. Ол санның ондықтары мен

бірліктерін қандай цифрлар көрсетеді?

Кестедегі цифрлардың жазылу реті туралы не айтуға болады?

Екі таңбалы сандарды кестедегі түрде жазып қосқан дұрыс. Оны баған түрінде немесе жазбаша қосу дейміз. Сонда: а) Ондықтар ондықтардың астына, ал бірліктер бірліктердің астына жазылады. Жазу үлгісі:

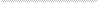8-ді бірліктердің астына жазады.

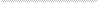б) Ондықтарды қосады: 4 + 2 = 6.

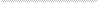6 – ны ондықтардың астына жазады.

в) Жауапты оқиды: қосындының мәні 68 – ге тең.

Кестелік қосудың қандай теңдіктерін қолдандық? Жаз.

3. Кестенің бірінші қатарындағы санды оқы.

Ол санның ондықтары мен бірліктерін қандай

цифрлар көрсетеді? Кестенің екінші қатарын-

дағы санды оқы. Ол санның ондықтары мен

бірліктерін қандай цифрлар көрсетеді?

Кестедегі цифрларлың жазылу реті туралы не айтуға болады? Екі таңбалы сандарды кестедегі түрде жазып, азайтқан тиімді. Оны баған түрінде немесе жазбаша азайту дейміз. Сонда:

а) Ондықтарды ондықтардың астына, ал бірліктерді бірліктердің астына жазады.

ә) Бірліктерді бірліктерден азайтады: 8 – 3 = 5.

5 – ті бірліктердің астына жазады.

в) Жауапты оқиды: айырманың мәні 45 – ке тең.

Кестелік азайтудың қандай теңдіктерін қолдандық?

Жаз.

4. Екі таңбалы сандарды қосу мен азайтудың қалған жағдайлары да осы схемаға сәйкес енгізіледі:

1000 көлемінде қосу мен азайтудың жазбаша әдістері ауызша әдістерден кейін ашып айқындалады. Үш таңбалы сандарды қосу мен азайтудың жазбаша әдістерін меңгеру оларды кез келген шамадағы сандарға табысты түрде қолданудың шарты болып табылады. Алдымен қосудың, сонан соң азайтудың азбаша әдістері оқып үйреніледі.

Баған түрінде қосуды қосындыны қосындымен қосу ережесі пайдаланылады. Бұл ережені балаларды қосудың жазбаша әдісімен таныстырудан бұрын қайталап алады. Ол үшін мына түрдегі мысалдар шығарылады: (8 + 7) + (2 + 3) немесе (20 + 4) + (10 + 6). Оқушылар нәтижені басқа қандай түрде орындауға болатындығын естеріне түсіреді. [33] Сонан соң ереже бірнеше орындауға болатындығын естеріне түсіреді. Сонан соң ереже бірнеше қосылғыштардың қосындысын 1000 көлеміндегі сандармен қосуға қолданылады, мысалы:

(300 + 40 + 5) + (200 + 20 + 4) = (300 + 200) + (40 + 20) + (5 + 4) = 569

(300 + 40 + 5) + (200 + 4) = (300 + 200) + 40 (5 + 4) = 549

(300 + 40 + 5) + (20 + 4) = 300 +(40 + 20) + (5 + 4) = 369

Осындай бірнеше мысал шығарып, балалар жүздіктерді жүздіктермен, ондықтарды ондықтармен, бірліктерді бірліктермен қосу ыңғайлы болатынын байқайды. Мұнда қандай сандар қосылғанын анықтаған пайдалы (345 пен 224, 345 пен 204, 345 пен 24).

Баған түрінде қосудың жалпыға белгілі жазылуының жазбаша әдісін енгізу үшін осындай дайындық жұмысы толық жеткілікті. Оқушылар осылайша жазудың орынды болатынын түсінеді – мұнда қосу тез орындалады, өйткені аралық нәтижелер табысымен әрқайсысы өз орнына жазылады.

Жазбаша қосу мынадай ретпен қарастырылады: 1) бірліктерінің қосындысы мен ондықтарының қосындысы 10-нан кіші (кем) болатын жағдайлар; 2) бірліктерінің қосындысы мен ондықтарының қосындысы (немесе екі қосынды да) 10-ға тең болатын жағдайлар; 3) бірліктерінің қосындысы мен ондықтарының қосындысы (немесе қосындының екеуі де) 10-нан үлкен (артық) болатын жағдайлар.

Алдымен ондытан аттамай қосуға мысалдар шығарылады: 232 + 347, 235 + 43. Оқушылар алғашқы кезде есептеу әдісін бір жолға тәптіштеп жаза отырып, ауызша шығарады, сонан кейін мұғалім бұл мысалдарды баған түрінде мынадай түсінік бере отырып жазып көрсетеді: екінші санның бірліктерін бірінші санның бірліктерінің астына келтіріп, ондықтарын ондықтарының астына келтіріп, жүздіктерін жүздіктердің астына келтіріп жазады. Қосу әдісіне түсінік беріледі:

2 бірлікке 7 бірлікті қосамыз, 9 бірлік шығады. Қосындыда

232 9-ды сызықшаның астыңғы жағына бірліктердің орнына

+ жазамыз; 3 ондыққа, 4 ондықты қосамыз, 7 ондық болады.

347 Қосындыда ондықтардың орнына 7-ні жазамыз. Екі жүздікке 3

жүздікті қосамыз, 5 жүздік шығады. Қосындыда жүздіктердің

орнына 5 – ті жазамыз. Қосынды 579 – ға тең.

Балалар мысалдардың жазылуы мен түсінік беруге жаттығады, баған түрінде қосқанда бірліктерден бастайтынын есіне сақтап қалады.

427 + 133, 363 + 245, 236 + 464 түріндегі мысалдарды шығарғанда жазбаша қосуды ауызша қосудағыдай жоғарғы разрядтардан бастамай, І разряд бірліктерінен бастайтыны неліктен екенін көрсету оңай: қосуды жүздіктен бастап, балалар бір мысал (457 + 243) шығарып көрсін – олардың мұндай ретпен есептеудің ыңғайсыз екеніне көздері жетеді, өйткені жүздіктер мен ондықтар цифрларын түзетуге тура келеді. [34]

Ондықтан аттап қосуға берілген мысалдарды шығарудан бұрын қосу таблицасын қайталап алу мына түрдегі дайындық жұмыстарын енгізу қажет: 8 бірл. + 6 бірл., 6 онд. + 7 онд. Т.с.с., бұларда нәтижені ірірек бірліктермен өрнектеуге тура келеді. Алдыңғы кезеңдегідей, алдымен мысалдар толық түсінік беріліп шығарылады:

544 4 бірлікке 8 бірлікті қосамыз, 12 бірлік, немесе 1 ондық

+ пен 2 бірлік шығады. 2 бірлікті бірліктердің астына

218 жазамыз, ал бір ондықты ондықтарға қосамыз т.с.с.

Бірте-бірте қысқаша түсініктеме беруге көшу керек: 4 пен 8 – он екі, 2 – ні жазамын, 1 – ді ойда сақтаймын; 4 пен 1 – бес, тағы да 1 – алты, 6 – ны жазамын; 5 пен 2 – жеті, небары 762. Егер оқушы қате жіберсе, одан тәптіштеп түсініктеме беруді талап етеді.

Жазбаша қосуды оқып үйренудің қорытынды сабақтарында оқушылар бірнеше қосылғыштарды қосудың жазылу формасымен және пайымдауымен танысады.

Оқушылар жазбаша қосуды орындау әдісін меңгерумен қоса, берілген тақырыпты оқып үйренудің барлық кезеңдерінде тез және дұрыс есептеулер д а ғ д ы с ы н қалыптастыруға тырысу қажет. Осы мақсатпен әр түрлі жаттығулар: мысалдар, есептер, теңдеулер шығару т.с.с жеткілікті мөлшерде енгізіледі.

Оқушылар жазба есептеулермен қатар ауызша есептеулерге төселуі үшін мынадай тапсырмалар берген пайдалы: “Мысалдардың шешулерін ауызша шығару қиын болғанда ғана, баған түрінде жазыңдар (мысалы:х – 290 = 610, х – 295 = 638, х – 295 = 605)”.

Азайтудың жазбаша әдістерімен істелетін жұмыс осыған ұқсас жүргізіледі. Ең алдымен қосындыны қосындыдан шегеру ережесі қарастырылады, ал сонан соң жазбаша азайту әдісі ашылып айқындалады. Алғашқы рет азайтудың мына түрдегі ең оңай жағдайлары енгізіледі: 563 – 321. Балаларға нәтижелерді ауызша тапқызып, есептеу әдісін тәптіштеп жазу ұсынылады.

563 – 321 = (500 + 60 + 3) – (300 + 20 + 1) =

= (500 – 300) + (60 – 20) + (3 – 1) = 242

Қосу амалындағыдай, мысалды баған түрінде жазса, нәтижені табу оңайырақ және тезірек болатынын балалар байқайды.

Алғашқы кезде азайтуды тәптіштеп жазып орындайды, сонан соң қысқаша түсініктемелер енгізіледі.

Бұдан кейін мына түрдегі жағдайлар қарастырылады (574 – 304, 547 – 340, 507 – 304). Оларды енгізуден бұрын нолі бар амалдарды қайталап алған дұрыс ( 5 + 0, 5 – 0, 0 – 0, 7 · 0 – 0, 0 : 9 + 0 т.с.с).

Бұдан кейін мына түрдегі жағдайлар қарастырылады: 540 – 126 және 603 – 281.

Алдын ала разрядтық бірліктердің арасындағы қатыстарды қайталап алу керек. (1 ондықта неше бірлік бар? 1 жүздікте неше ондық бар?) Ең алдымен мысалдар тәптіштеп түсініктеме беріле отырып шығарылады:

540 “Біз нольден 6 бірлікті шегеруімізге болмайды, 4 ондытың

– 1 ондығын аламыз. Алғанымызды ұмытып қалмау үшін, 4

126 цифрының бөбесіне нүкте қоямыз. 1 ондықта 10 бірлік бар

10- нан 6 – ны шегереміз. 4 бірлік қалады. Жауабын

бірліктердің астына жазамыз. 3 ондықтан 2 ондықты

шегереміз, 1 ондық қалады т.с.с. ” 603 – 281 мысалының шешуін осылайша түсіндіреді, мұнда 1 жүздікті “қарызға алуға” оны ондықтарға ұсақтап, 10 ондықтан 8 ондықты шегеруге тура келеді. Жүздіктер цифрының (6) төбесіндегі нүкте бір жүздік алынғанын және 5 жүздік қалғанын көрсетеді.

Содан кейін мына түрдегі мысалдар: 875 – 528, 628 – 365, және, ақырында, мына түрдегі мысалдар енгізіледі: 831 – 369. Осы мысалдардың бәрінде көршілес жоғарғы разрядтың бірлігін “қарызға алуға” (бір немесе екі рет) тура келеді. Дайындық жаттығулары ретінде азайтудың таблицалық жағдайларын қайталап алып, 1 онд. 6 бірл. – 7 бірл., 1 ж. 5 онд. – 8 онд. т.с.с. ауызша тапсырмалар енгізген пайдалы болады. Сондай-ақ разрядтық бірліктердің қатыстарын және жоғарғы разряд бірліктерін көршілес төменгі разряд бірліктеріне түрлендіруді қайталап алған жөн.