Средняя квадратическая погрешность. Предельная и относительная погрешность.
Среднее арифметическое из случайных погрешностей не может объективно характеризовать точность измерений, так как на его величину оказывают влияние знаки случайных ошибок (происходит компенсация) и кроме того она не отражает влияние отдельных больших по абсолютной величине ошибок. Поэтому для оценки точности ряда равноточных измерений l1; l2; … ln одной и той же величины Х, сопровождающейся случайными погрешностями ∆1, ∆2, , , , , , ∆n, пользуется средней квадратичной ошибкой m, равной:
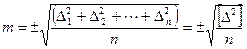
Пример: дан ряд случайных ошибок измерений некоторой величины: +4, - 2, 0, -4, +3.

Предельной погрешностью называют такое наибольшее по абсолютной величине значение случайной ошибки, которой она может достигнуть при данных условиях измерений. Установлено, что случайная ошибка может достигать удвоенной средней квадратической ошибки в пяти случаях из ста, утроенной – в трех из тысячи. Поэтому за предельную ∆пр. принимают утроенную среднюю квадратическую ошибку ∆пр. = 3m.
Относительной ошибкой называют отношение абсолютной ошибки к измеренной величине. Она выражается простой дробью, числитель которой равен единице. Обычно относительной ошибкой характеризуют линейные измерения.
Например, измерена линия длиной l=221,16 с абсолютной ошибкой ∆=0,11 м.
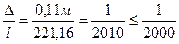
Дата добавления: 2015-11-18; просмотров: 1511;
