Графический способ.

а) Определение площади при помощи палетки. Точность этого способа 1/50 к площади определенной аналитическим путем. Палетка – это сетка квадратов, нанесенная на прозрачной основе.

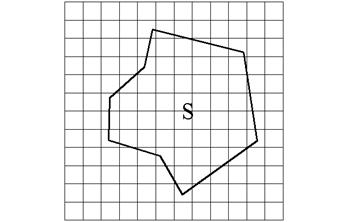
	Палетку накладывают на контур (Рис. 4.9), площадь которого определяют как количество полных и неполных квадратов (дополняя их до полных). Площадь S определяют по формуле S = f n, где f - площадь одного квадрата с учетом масштаба плана, n – число квадратов.
Рис.4.9. Графический способ

б) Способ геометрических фигур. Участок, площадь которого определяют, разделяют на фигуры, площадь которых можно определить по формулам геометрии (треугольники, трапеции и др.). Измеряют основание,высоту и вычисляют площадь с точностью 1/100 к площади определенной аналитическим способом.

в) Механический способ. Площадь определяют с помощью планиметра. Точность этого способа от 1/200 до 1/400 к площади, определенной аналитическим методом.

Планиметр состоит из двух рычагов – полюсного и обводного. Полюсный рычаг на одном конце имеет груз с иглой накалываемой на бумагу, а на другом конце - штифт с круглой головкой, вставляемой во втулку обводного рычага.

Обводной рычаг представляет собой металлическую линейку с миллиметровыми делениями. На одном конце рычага имеется обводной шпиль (или стеклышко с точкой посредине) и ручка. На обводном рычаге имеется каретка со счетным механизмом, которую можно перемещать вдоль рычага и зажать в определенном положении. Это положение можно зафиксировать отсчетом по верньеру на каретке механизма.

На рисунке 4.10 показан отсчет по счетному механизму планиметра. Этот отсчет равен 4558. Для определения площади участка, обводной шпиль ставят в любую точку на контуре, а полюс- вне контура (между рычагами в начальном положении угол должен быть близким к 90⁰) и берут отсчет по счетному механизму n₁, например 4558.

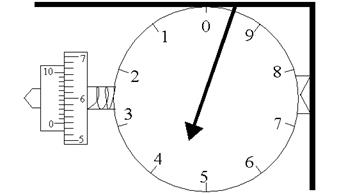
	Затем ведут обводной шпиль по контуру фигуры вправо по ходу часовой стрелки и возвращаются в исходную точку, где снова берут отсчет n2, например 6769. Вычитая из второго отсчета первый получают площадь обведенной фигуры в делениях планиметра S = n2 - n1 = 6769 –4558 =2211
Рис.4.10. Планиметр

Для получения площади этой фигуры в квадратных метрах необходимо полученную площадь в делениях планиметра умножить на цену деления планиметра - С, тогда S = с(n₂ -n₁).

При определении площади с полюсом внутри контура фомула будет иметь такой вид.

S = с(n₂ -n₁+ Q), где Q – постоянное число планиметра.

Для определения цены деления планиметра с вычерчивают в данном масштабе квадрат. Вычисляют его площадь с учетом масштаба. Так, например, масштаб плана 1:1000, а сторона квадрата 10 см, тогда площадь его на местности равна 10000 м². Определив площадь его в делениях планиметра при обводе с полюсом вне контура, вычисляют цену деления.

C = S _{В КВ. М} / S _{В ДЕЛ. ПЛАН.} = 10000 м² / 1000 = 10 м²

Для большей уверенности разностиn₂ -n₁ получают несколько раз и если они не отличаются более чем на 4-5 делений, то берут среднее из них.

Таблица 4.3.

Отсчеты	Разности отсчетов	Средние разности отсчетов
n3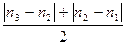
n2	n3 – n2
n1	n2 – n1

Для определения постоянного числа планиметра Q обводим площадь какой-либо фигуры с полюсом вне фигуры и получаем первую разность отсчетов n₂ -n_{1 .} Потом устанавливаем полюс внутри той же фигуры и после обвода получаем вторую разность отсчетов n₂^I -n₁^I.Вычитая из первой разности вторую получаем q в делениях планиметра q = (n₁ – n₂) - (n₁^I – n₂^I), а значение Q определяем по формуле Q = сq.

Решение задач на топографических картах и планах.

При разработке проектов планировки и застройки населенных пунктов на картах и планах могут решаться следующие задачи:

· определение географических координат точек;

· определение прямоугольных координат точек;

· определение длин линий;

· определение ориентирных углов;

· определение высот точек;

· определение крутизны скатов;

· построение профиля местности по заданному направлению;

· проектирование по карте горизонтальных и наклонных площадок.