Их применение на производстве

Числовые значения случайных событий называются случайными величинами. Они распределяются по определенным математическим законам, которые графически представляются в виде различных кривых. Как известно, при обработке заготовок неизбежны погрешности, и поэтому нельзя получить у всех изготовленных деталей точно один и тот же заданный размер. Появление того или иного размера у очередной изготовляемой детали является случайным событием, а значение самого размера будет случайной величиной. Случайные величины обладают определенными закономерностями, которые можно установить при большом количестве наблюдений и при знании основных приемов обработки результатов наблюдений.

Так, на основе анализа размеров 200 деталей, изготовленных при соблюдении технологического процесса, невозможно установить какой-либо закономерности в распределении размеров данной партии. Для этого нужно построить ряды частот, т. е. определить частоту появления определенного размера и диаграмму распределения. Если на графике отложить, по горизонтальной оси (Х) интервалы размеров, а по вертикальной ( 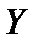) — частоту повторения деталей (количество их), то характер распределения всей партии деталей наглядно представится столбиковой диаграммой, называемой. Соединив середины высот прямоугольников на диаграмме, получим практическую кривую распределения размеров, которая называется полигоном распределения.

Анализ рядов частот и формы полученной кривой показывают, что распределение размеров деталей, как случайных величин, имеет определенную закономерность. Например, больше всего деталей имеют размеры, близкие к размерам среднего интервала. Чем меньше и больше размеры деталей, тем реже они повторяются.

Многочисленными измерениям деталей, изготовленных по разным технологическим процессам (на станках, автоматах, полуавтоматах и др.), установлено, что при обработке, распределение размеров соответствует широко известному закону нормального распределения случайных величин. Этот закон выражен кривыми колокообразного вида называемыми кривыми Гаусса (по фамилии немецкого ученого).

Характерными особенностями закона нормального распределения случайных величин является то, что центром распределения случайных величин является их среднее значение, что появление случайных величин с одинаковыми отклонениями от среднего, но с разными знаками (в « + » и в «—»), равновероятно. Чем меньше и чем больше значение случайных величин, тем реже они встречаются.

Установив, что распределение размеров деталей подчиняется закону нормального распределения, используют особенности этого закона для определения точности технологических, процессов. Для этого после изготовления партии деталей измеряют их размеры и определяют два основных показателя закона распределения: среднее арифметическое значение и среднее квадратическое отклонение от среднего (сигма).

.Среднее арифметическое значение определяемое по формуле

,

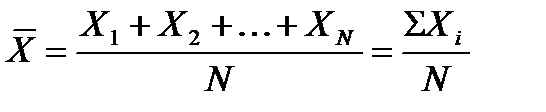где 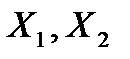и т. д. - размеры отдельных деталей; 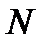- общее количество деталей; 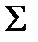- знак суммы.

Среднее, квадратическое отклонение от среднего определяется по формуле

= ,

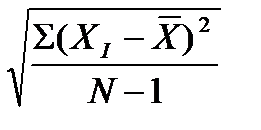где 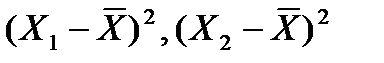и т. д. - разности между размером каждой детали и средним арифметическим размером. Среднее арифметическое значение размеров характеризует центр, вокруг которого группируются размеры при данном методе обработки. Среднее квадратическое отклонение является количественной характеристикой рассеивания размеров при обработке, и поэтому по значению величины оценивают точность технологического процесса. Чем круче будет кривая, тем меньше значение и, следовательно, точнее будет технологическим процесс.

Если площадь кривой ограничить в пределах +3 и -3 , то по расчетам теории вероятностей 99,73 % площади будет находиться в заданной зоне и 0,27 % будет находиться за пределами ±3 .

Поэтому при сравнении величины допуска на обработку по чертежу с точностью технологического процесса принимают, чтобы допуск был не менее 6 .

Для ориентировочного определения точности технологического процесса или правильности настройки станка нужно изготовить 10—30 деталей.

Для анализа технологического процесса обращают внимание не только на разброс погрешностей изготовленных деталей, но и на значение среднего арифметического. При правильно построенном технологическом процессе необходимо, чтобы среднее арифметическое значение совпадало с серединой поля допуска, и если разброс размеров, т. е. ±3 , равен допуску, то можно надеяться, что процент брака деталей будет ничтожно малый (не менее 0,27 %).

Кроме закона нормального распределения случайных величин существуют другие математические законы распределения случайных величии, но применительно к размерам изготовляемых деталей они применяются на производстве очень редко, кроме закона существенно положительных величин.

По закону существенно положительных величин который известен в математике как закон Максвелла, распределяются величины отклонений формы и расположения поверхностей: отклонений от круглости, неперпендикулярности, торцовое и радиальное биение, биение начальной окружности зубчатых колес и др.

Форма кривой Максвелла по горизонтальной оси располагаются величины отклонений нуля, а по вертикальной оси частота их появления. Применительно к торцовому биению, что представляется так: какое-то количество деталей не имеют биения (оно равно нулю), затем с увеличением значения биения увеличивается и частота их повторения. В зависимости от точности технологического процесса увеличение частоты повторения биений ограничивается определенным пределом величины биения 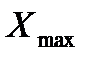. При дальнейшем повышении величины биения количество деталей с такими величинами биения уменьшается. Теоретическая область величины биения от нуля до бесконечности.

Показателем точности технологического процесса по отклонениям формы и расположения поверхностей обрабатываемых деталей также является среднее квадратическое отклонений 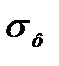. Если определить, измерением величины отклонений формы у 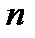деталей, то значение показателя точности процесса можно подсчитать по формуле

,

где - среднее арифметическое значение из полученных величин отклонений формы.

Расположение отклонений на кривой Максвелла одностороннее и, по расчетам теории вероятностей, 99,73% всей площади кривой ограничивается величиной, равной 5,25 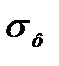. За пределом 5,25 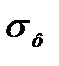, будет всего 0,27 % площади. Следовательно, если допуск на отклонение формы детали установить равным 5,25 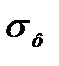, то вероятность годных деталей (с отклонениями, равными и меньше величины 5,25 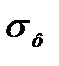) будет равна 99,73%, а вероятность брака, т. е. количества деталей с отклонениями формы больше 5,25 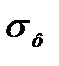, будет всего 0,27%.