Тема 5. Інтеграл і його застосування
5.1. Для функції  знайдіть хоча б одну первісну:
знайдіть хоча б одну первісну:
1) 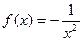 ;2)
;2) 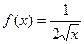 ;3)
;3) 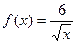 ;
;
4) 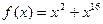 ;5)
;5) 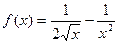 ;6)
;6) 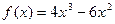 ;
;
7) 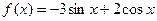 ;8)
;8) 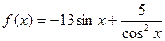 ;9)
;9) 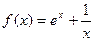 ;
;
10) 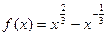 ;11)
;11) 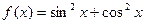 ;12)
;12) 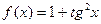 ;
;
13) 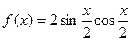 ;14)
;14) 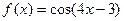 ;15)
;15) 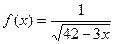 .
.
5.2. Знайти для функції первісну, графік якої проходить через дану точку:
1) 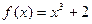 , М (2; 15); 2)
, М (2; 15); 2) 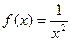 , М (1; 1);
, М (1; 1);
3) 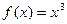 , А (2; 1); 4)
, А (2; 1); 4) 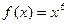 , М (1; 1);
, М (1; 1);
5) 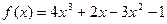 , М (1; -1); 6)
, М (1; -1); 6) 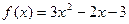 , А (3; 9);
, А (3; 9);
7) 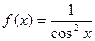 , М (
, М ( 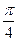 ; -1); 8)
; -1); 8) 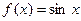 , М (
, М ( 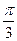 ;
; 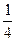 );
);
9) 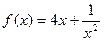 , М (1; 4); 10)
, М (1; 4); 10) 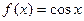 , М (
, М ( 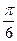 ; 1).
; 1).
5.3. Обчисліть невизначений інтеграл:
1) 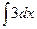 ;2)
;2) 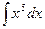 ; 3)
; 3) 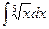 ;
;
4) 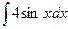 ; 5)
; 5)  ; 6)
; 6) 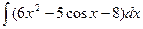 ;
;
7) 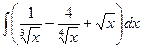 ; 8)
; 8) 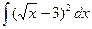 ; 9)
; 9) 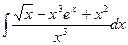 ;
;
10) 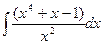 ; 11)
; 11) 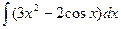 ;12)
;12) 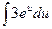 ;
;
13) 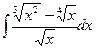 ; 14)
; 14) 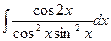 ; 15)
; 15) 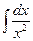 ;
;
16) 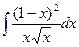 ; 17)
; 17) 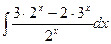 ; 18)
; 18) 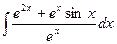 ;
;
19) 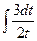 ; 20)
; 20) 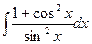 ; 21)
; 21) 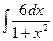 ;
;
22) 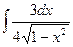 ; 23)
; 23) 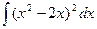 ; 24)
; 24) 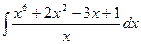 ;
;
25) 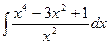 ; 26)
; 26) 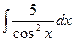 ; 27)
; 27) 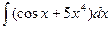 ;
;
28) 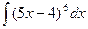 ; 29)
; 29) 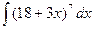 ; 30)
; 30) 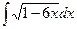 ;
;
31) 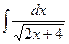 ; 32)
; 32) 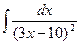 ; 33)
; 33) 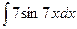 ;
;
34) 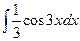 ; 35)
; 35) 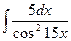 ; 36)
; 36) 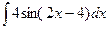 ;
;
37) 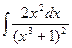 ;38)
;38) 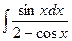 ; 39)
; 39) 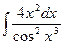 ;
;
40) 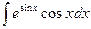 ; 41)
; 41) 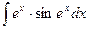 ;42)
;42) 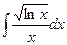 ;
;
43) 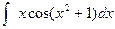 ; 44)
; 44) 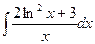 ; 45)
; 45) 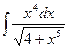 ;
;
46) 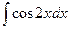 ; 47)
; 47) 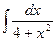 ; 48)
; 48) 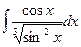 ;
;
49) 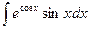 ;50)
;50) 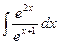 ; 51)
; 51) 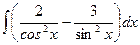 ;
;
52) 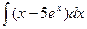 ; 53)
; 53) 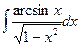 ; 54)
; 54) 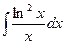 ;
;
55) 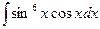 ;56)
;56) 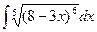 ; 57)
; 57) 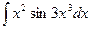 ;
;
58) 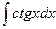 ; 59)
; 59) 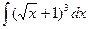 ; 60)
; 60) 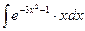 ;
;
61) 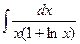 ;62)
;62) 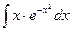 ; 63)
; 63) 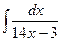 ;
;
64) 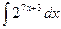 ; 65)
; 65) 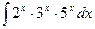 ;66)
;66) 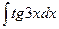 ;
;
67) 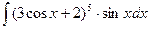 ; 68)
; 68) 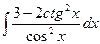 ; 69)
; 69) 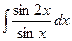 ;
;
70) 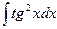 ; 71)
; 71) 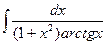 ; 72)
; 72) 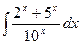 ;
;
73) 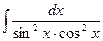 ;74)
;74) 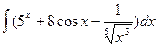 ; 75)
; 75) 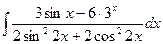 ;
;
76) 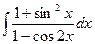 ; 77)
; 77) 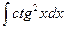 ;78)
;78) 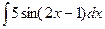 ;
;
79) 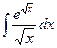 ;80)
;80) 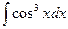 ; 81)
; 81) 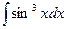 ;
;
82) 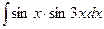 ;83)
;83) 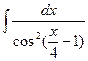 ; 84)
; 84) 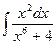 ;
;
85) 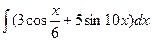 ; 86)
; 86) 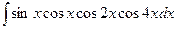 ; 87)
; 87) 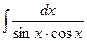 ;
;
88) 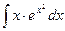 .
.
5.4. Обчисліть визначені інтеграли:
1) 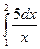 ; 2)
; 2) 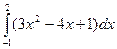 ; 3)
; 3) 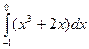 ;
;
4) 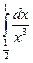 ; 5)
; 5) 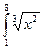 ; 6)
; 6) 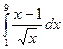 ;
;
7) 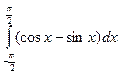 ; 8)
; 8) 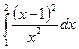 ; 9)
; 9) 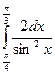 ;
;
10) 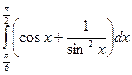 ; 11)
; 11) 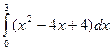 ; 12)
; 12) 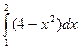 ;
;
13) 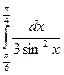 ; 14)
; 14) 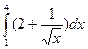 ; 15)
; 15) 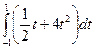 ;
;
16) 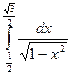 ; 17)
; 17) 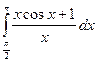 ;18)
;18) 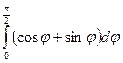 ;
;
19) 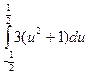 ; 20)
; 20) 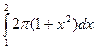 ; 21)
; 21) 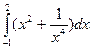 ;
;
22) 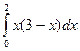 ; 23)
; 23) 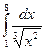 ; 24)
; 24) 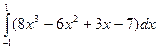 ;
;
25) 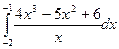 ; 26)
; 26) 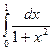 ; 27)
; 27) 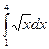 ;
;
28) 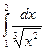 ; 29)
; 29) 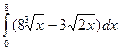 ; 30)
; 30) 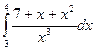 ;
;
31) 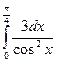 ; 32)
; 32) 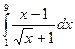 ; 33)
; 33) 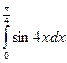 ;
;
34) 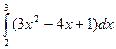 ; 35)
; 35) 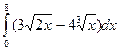 ; 36)
; 36) 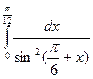 ;
;
37) 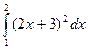 ; 38)
; 38) 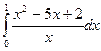 ; 39)
; 39) 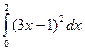 ;
;
40) 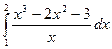 ; 41)
; 41) 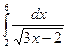 ; 42)
; 42) 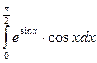 ;
;
43) 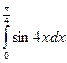 ; 44)
; 44) 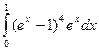 ; 45)
; 45) 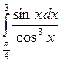 ;
;
46) 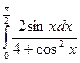 ; 47)
; 47) 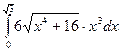 ; 48)
; 48) 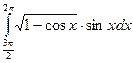 ;
;
49) 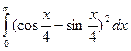 ; 50)
; 50) 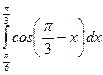 ; 51)
; 51) 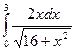 ;
;
52) 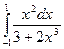 ; 53)
; 53) 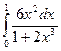 ; 54)
; 54) 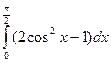 ;
;
55) 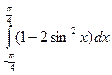 ; 56)
; 56) 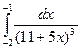 ; 57)
; 57) 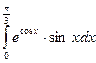 ;
;
58) 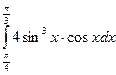 ; 59)
; 59) 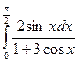 ; 60)
; 60) 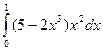 ;
;
61) 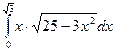 ; 62)
; 62) 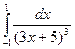 ; 63)
; 63) 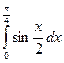 ;
;
64) 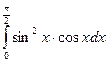 ; 65)
; 65) 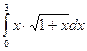 ; 66)
; 66) 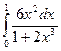 ;
;
67) 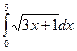 ; 68)
; 68) 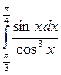 ; 69)
; 69) 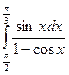 ;
;
70) 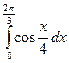 ; 71)
; 71) 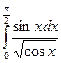 ; 72)
; 72) 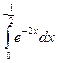 ;
;
73) 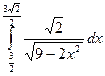 ; 74)
; 74) 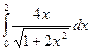 ; 75)
; 75) 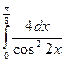 ;
;
76) 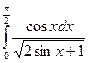 ; 77)
; 77) 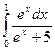 ; 78)
; 78) 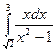 ;
;
79) 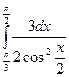 ; 80)
; 80) 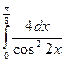 ; 81)
; 81) 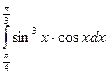 ;
;
82) 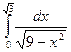 ; 83)
; 83) 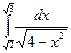 ; 84)
; 84) 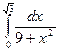 ;
;
85) 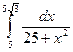 ; 86)
; 86) 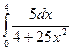 ; 87)
; 87) 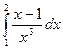 ;
;
88) 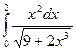 ; 89)
; 89) 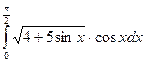 .
.
5.5. Знайти площу фігури, обмеженої лініями:
1) у = х2 + 2, у = 3; 2) у = х2, у = 0, у = 2 – х;
3) у = х2 – 9, у = 0; 4)у = х2 + 1, у = 0, х = 2, х = 0;
5) у = 6х – х2, у = 0; 6) у = х2 – 5х + 6, у = 0;
7) 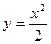 ,
, 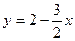 ; 8) у = 2х – х2, у = х;
; 8) у = 2х – х2, у = х;
9) у2 = х, х = 1, х = 4; 10) у = х2, у = -х + 6, у = 0;
11) у = х2 – 4х + 4, у = 4 – х; 12) у = 8 + 2х – х2, у = 2х + 4, у = 0;
13) у = cos x, х = 0, х = 2π, у = 0; 14) ху = 4, х + 4у – 10 = 0;
15) у = х2 – 1, у = 3; 16) у = 5 – х2, у = 1;
17) 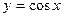 , х = 0, у = 0,
, х = 0, у = 0, 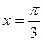 ; 18) у = х2 + 1, х = 2, х = 0, у = 0;
; 18) у = х2 + 1, х = 2, х = 0, у = 0;
19) у = -х2, у = х – 2; 20) у = -х2 + 3, х = -1, х = 1,5;
21) у = -х2 + 4, у = х2 - 4; 22) у = х2 – 4х, у = х – 4;
23) у = 2х2, у = х; 24) 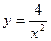 , х = 1, х = 2;
, х = 1, х = 2;
25) 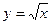 , у = х2; 26) у = 7х – 2х2,
, у = х2; 26) у = 7х – 2х2, 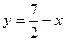 ;
;
27) у = х, у = 4 – х, х = 0; 28) у = 1 – х, у = 3 – 2х – х2;
29) 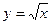 , ху = 1, х = 4, у = 0; 30) у = -х2 + 5, у = х2 + 1;
, ху = 1, х = 4, у = 0; 30) у = -х2 + 5, у = х2 + 1;
31) 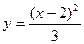 , у = х + 4; 32) ху = 7, у = 0, х = 2, х = 6;
, у = х + 4; 32) ху = 7, у = 0, х = 2, х = 6;
33) у = х, 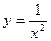 , х = 2; 34)
, х = 2; 34) 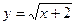 ,
, 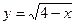 , у = 0;
, у = 0;
35) у = 8х – х2 – 7, вісь Ох; 36) у2 = 4х, х2 = 4у;
37) 4у = х + 2, у = 3 – х, у = 0.
5.6. Обчислити об’єм тіла, утвореного обертанням навколо вісі Ох фігури, що обмежена лініями:
1) у = х2, х = 0, х = 2, у = 0; 2) 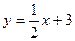 , у = 0, х = 2;
, у = 0, х = 2;
3) у2 = 8х, у = х2; 4) ху = 4, х = 3, х = 12 та віссю абсцис;
5) у = 0, х = 0, х = 2, у = х + 1; 6) 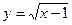 , у = 0 і х = 4;
, у = 0 і х = 4;
7) ху = 8, у = 0, х = 1 і х = 6; 8) 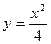 , х = 4 та віссю Ох;
, х = 4 та віссю Ох;
9) у = 2 + х2, х = 1, х = 2, у = 0; 10) у2 – 3х = 0, х – 3 = 0;
11) 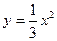 , у = 0, х – 3 = 0, х = 3; 12) у = х3, х = 1, х = 2.
, у = 0, х – 3 = 0, х = 3; 12) у = х3, х = 1, х = 2.
5.7. Обчислити об’єм тіла, утвореного обертанням навколо вісі Оу фігури, що обмежена лініями:
1) у = х2, у = 1, у = 3; 2) у = х2 + 1, у = 4;
3) 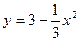 , у = 2, у = 0; 4) х2 – 2у = 0, у – 2 = 0;
, у = 2, у = 0; 4) х2 – 2у = 0, у – 2 = 0;
5) ху = 6, у = 1, у = 4 та віссю Оу; 6) у = 6х2, у = 3 та віссю Оу;
7) 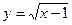 , у = 0, у = 3; 8) ху = 8, х = 0, у = 1 і у = 6;
, у = 0, у = 3; 8) ху = 8, х = 0, у = 1 і у = 6;
9) 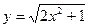 , віссю Оу і у = 7; 10)
, віссю Оу і у = 7; 10) 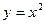 ,
, 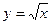 ;
;
11) у = х3, х = 0, у = 0, у = 8; 12) у = 2х, х = 0, у = 5.
5.8. Знайти об’єм кульки, радіуса 5 см.
5.9.Тіло рухається з прискоренням а = 24t2 + 8. Знайти закон руху, якщо: t = 1с, V = 10 м/с, S = 12 м.
5.10. Тіло рухається зі швидкістю V (t) = 6t + 4 (м/с). Знайти шлях, пройдений тілом за третю і п’яту секунду.
5.11. Тіло рухається зі швидкістю V (t) = 4t3 +2t + 3 (м/с). Знайти шлях, пройдений тілом:
1) за третю секунду; 2) за три секунди від початку руху.
5.12. Тіло рухається зі швидкістю V (t) = 4t – t2 (м/с). Знайти шлях, пройдений тілом від початку руху до зупинки.
5.13. Знайдіть відстань, пройдену точкою за проміжок часу від t = 0 до t = 3 с, якщо швидкість точки змінюється за законом V = 9,8t – 0,3t2.
5.14. Швидкість прямолінійного руху точки змінюється за законом V (t) = 3t2 – 2t. Знайдіть закон руху точки.
5.15. Матеріальна точка рухається зі швидкістю V (t) = sin t + cos t. Знайдіть рівняння руху точки, якщо при 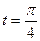 пройдений шлях дорівнює 3 м.
пройдений шлях дорівнює 3 м.
5.16. Тіло рухається по прямій зі швидкістю V (t) = 4t + 2 (t – час у секундах, V – швидкість у м/с). Знайдіть довжину шляху, який пройшло тіло за перші 3 с.
5.17. Швидкість руху тіла задано рівнянням V = (3t2 + 2t - 1) (м/с). Знайти шлях, який пройде тіло за 10 с від початку руху.
5.18. Тіло рухається прямолінійно зі швидкістю V (t) = 6t – 2t2 (м/с). Знайти шлях, пройдений тілом від початку руху до його зупинки.
5.19. Тіло кинули з поверхні Землі вертикально вверх зі швидкістю V = 39,2 – 9,8t (м/с). Знайти найбільшу висоту підйому тіла.
5.20. М’яч кинутий вертикально вгору з початковою швидкістю 20 м/с. На яку найбільшу висоту він підніметься?
5.21. Швидкість руху тіла 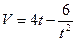 см/с. Визначити його шлях за четверту секунду.
см/с. Визначити його шлях за четверту секунду.
5.22. Точка рухається по прямій зі сталим прискоренням 12 м/с2. Знайти швидкість руху точки, якщо в початковий момент швидкість V0 = 100 м/с.
5.23. Точка рухається по прямій зі сталим прискоренням 8 м/с2. Знайти рівняння руху, якщо відомо, що в момент часу t = 0 точка знаходилась на відстані 24 м від початкового положення і мала початкову швидкість 5 м/с.
5.24. Швидкість руху точки задається рівнянням V = 7t2 – 1 (м/с). Знайти рівняння руху, якщо S = 12 м у момент часу t = 2с.
5.25. Швидкість руху задається рівнянням V = 3cos t (м/с). Знайти рівняння руху, якщо в початковий момент часу точка знаходилась на відстані 2 м від початкового положення.
Тестові завдання до теми
Дата добавления: 2015-09-11; просмотров: 1563;
