Методы перевода чисел
Числа в разных системах счисления можно представить следующим образом:
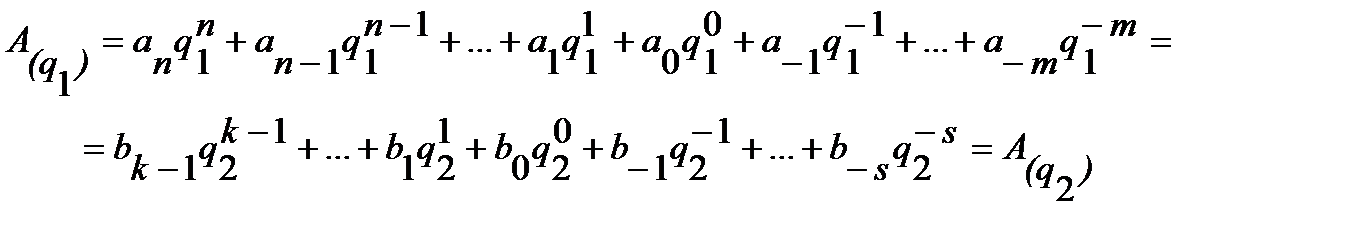
, где
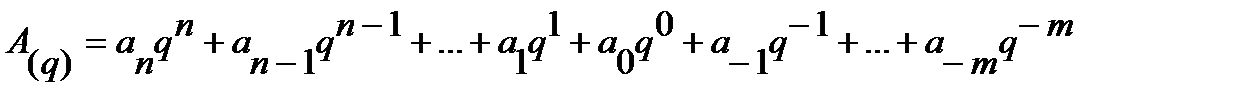
Значит, в общем виде задачу перевода числа из системы счисления с основанием q1 в систему счисления с основанием q2 можно представить как задачу определения коэффициентов bj нового ряда, изображающего число в системе с основанием q2. В такой постановке задачу перевода можно решить подбором коэффициентов bj.
Перевод чисел делением на основание новой системы
Перевод целых чисел осуществляется делением на основание q2 новой системы счисления, правильных дробей – умножением на основание q2. Действия деления и умножения выполняются по правилам q1-арифметики. Перевод неправильных дробей осуществляется раздельно по указанным правилам, результат записывается в виде новой дроби в системе с основанием q2.
Пример 1. Перевести десятичное число A = 6110 в систему счисления с q = 2.
61 | 2
6030 | 2
b0 = 1 3015 | 2
b1 = 0 14 7 | 2
b2 = 1 63 | 2
b3 = 1 2 1 = b5
b4 = 1
Ответ: 6110 = 1111012.
Табличный метод перевода
В простейшем виде табличный метод заключается в следующем: имеется таблица всех чисел одной системы с соответствующими эквивалентами из другой системы; задача перевода сводится к нахождению соответствующей строки таблицы и выбору из нее эквивалента. Такая таблица очень громоздка и требует большой емкости памяти для хранения.
Другой вид табличного метода заключается в том, что имеются таблицы эквивалентов в каждой системе только для цифр этих систем и степеней основания (положительных и отрицательных); задача перевода сводится к тому, что в выражение ряда (1) для исходной системы счисления надо поставить эквиваленты из новой системы для всех цифр и степеней основания и произвести соответствующие действия (умножения и сложения) по правилам q2-арифметики. полученный результат этих действий будет изображать число в новой системе счисления.
Пример 2. Перевести десятичное число A = 113 в двоичную систему счисления, используя таблицу эквивалентов цифр и степеней основания
(q2 = 2).
Таблица 1 – Таблица эквивалентов
| Десятичное число | Двоичное число |
| 100 | |
| 101 | |
| 102 | 110 0100 |
Решение. Подставив значения двоичных эквивалентов десятичных цифр и степеней основания в (3), получим
A = 113 = 1 · 102 + 1 · 101 + 3 · 100 = 001 · 1100100 + 0001 · 1010 + 0011 · 0001 = 11100012.
Ответ: 11100012.
Дата добавления: 2015-11-10; просмотров: 2217;
