Определение количества информации на основе вероятностного подхода

При определении количества информации на основе вероятностного подхода рассматриваем вероятность некоторого события как величину, которая может принимать значения от нуля до единицы. Вероятность невозможного события равна нулю (например: “завтра Солнце не взойдет над горизонтом”), вероятность достоверного события равна единице (например: “Завтра солнце взойдет над горизонтом”).

Вероятность некоторого события определяется путем многократных наблюдений (измерений, испытаний). Такие измерения называют статистическими. И чем большее количество измерений выполнено, тем точнее определяется вероятность события.

Математическое определение вероятности звучит так: вероятность равна отношению числа исходов, благоприятствующих данному событию, к общему числу равновозможных исходов.

Рассмотренная выше формула Хартли определяет количество необходимой информации для выявления определенного элемента множества при условии, что все элементы равновероятны. Однако может быть так, что какие-то элементы более вероятны (чаще встречаются), а какие-то меньше. Например, в русском языке буква «а» употребляется чаще, чем буква «ю».

Существует множество ситуаций, когда возможные события имеют различные вероятности реализации. Например, если монета несимметрична (одна сторона тяжелее другой), то при ее бросании вероятности выпадения "орла" и "решки" будут различаться.

Формулу для вычисления количества информации в случае различных вероятностей событий предложил К. Шеннон в 1948 году. В этом случае количество информации определяется по формуле:

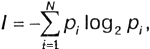(1),

где I - количество информации;

N - количество возможных событий;

р_i - вероятность i-го события.

Например, пусть при бросании несимметричной четырехгранной пирамидки вероятности отдельных событий будут равны:

р₁ = 1/2, р₂ = 1/4, р₃ = 1/8, р₄ = 1/8.

Тогда количество информации, которое мы получим после реализации одного из них, можно рассчитать по формуле (2.2):

I = -(l/2 log₂l/2 + l/4 log₂l/4 + l/8 log₂l/8 + l/8 log₂l/8) = (1/2 + 2/4 + 3/8 + 3/8) битов = 14/8 битов = 1,75 бита.

Этот подход к определению количества информации называется вероятностным.

Пример. На автобусной остановке останавливаются два маршрута автобусов: № 5 и № 7. Ученику дано задание: определить, сколько информации содержит сообщение о том, что к остановке подошел автобус № 5, и сколько информации в сообщении о том, что подошел автобус № 7.

Ученик провел исследование. В течение всего рабочего дня он подсчитал, что к остановке автобусы подходили 100 раз. Из них — 25 раз подходил автобус № 5 и 75 раз подходил автобус № 7. Сделав предположение, что с такой же частотой автобусы ходят и в другие дни, ученик вычислил вероятность появления на остановке автобуса № 5: p₅= 25/100 = 1/4, и вероятность появления автобуса № 7: p₇ = 75/100 = 3/4.

Отсюда, количество информации в сообщении об автобусе № 5 равно: i₅ = log₂4 = 2 бита. Количество информации в сообщении об автобусе № 7 равно:

i₇ = log₂(4/3) = log₂4 – log₂3 = 2 – 1,58496 = 0,41504бита.

Исходя из этого, можно сделать качественный вывод: чем вероятность события меньше, тем больше количество информации в сообщении о нем.

Количество информации о достоверном событии равно нулю. Например, сообщение “Завтра наступит утро” является достоверным и его вероятность равна единице. Из формулы (3) следует: 2ⁱ = 1/1 = 1. Отсюда, i = 0 бит.

Формула Хартли (1) является частным случаем формулы (3). Если имеется N равновероятных событий (результат бросания монеты, игрального кубика и т.п.), то вероятность каждого возможного варианта равна p = 1/N. Подставив в (3), снова получим формулу Хартли: 2ⁱ = N. Если бы в примере 3 автобусы № 5 и № 7 приходили бы к остановке из 100 раз каждый по 50, то вероятность появления каждого из них была бы равна 1/2. Следовательно, количество информации в сообщении о приходе каждого автобуса равно i = log₂2 = 1 биту. Пришли к известному варианту информативности сообщения об одном из двух равновероятных событий.

Пример. Рассмотрим другой вариант задачи об автобусах. На остановке останавливаются автобусы № 5 и № 7. Сообщение о том, что к остановке подошел автобус № 5, несет 4 бита информации. Вероятность появления на остановке автобуса с № 7 в два раза меньше, чем вероятность появления автобуса № 5. Сколько бит информации несет сообщение о появлении на остановке автобуса № 7?

Запишем условие задачи в следующем виде:

i₅ = 4 бита, p₅ = 2 · p₇

Вспомним связь между вероятностью и количеством информации: 2ⁱ = 1/p

Отсюда: p = 2^–i

Подставляя в равенство из условия задачи, получим:

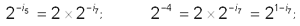
Отсюда:

Из полученного результата следует вывод: уменьшение вероятности события в 2 раза увеличивает информативность сообщения о нем на 1 бит. Очевидно и обратное правило: увеличение вероятности события в 2 раза уменьшает информативность сообщения о нем на 1 бит.

Контрольные вопросы:

1. Как измеряется информация при содержательном подходе?

2. Что такое алфавит?

3. Что называется мощностью алфавита?

4. Что называется объемом информации?

5. Как найти информационный вес символа?

6. Как рассчитать объем информации при равновероятносных событиях?

7. Как рассчитать объем информации при неравновероятносных событиях?

8. Что значит, информационный объем сообщения 1 бит?

9. Дайте определение понятию «энтропия» сообщения.