Двоичное кодирование числовой информации

Система счисления – это способ записи чисел. Обычно, числа записываются с помощью специальных знаков – цифр (хотя и не всегда). Если вы никогда не изучали данный вопрос, то, по крайней мере, вам должны быть известны две системы счисления – это арабская и римская. В первой используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и это позиционная система счисления. А во второй – I, V, X, L, C, D, M и это непозиционная система счисления.

В позиционных системах счисления количество, обозначаемое цифрой в числе, зависит от ее позиции, а в непозиционных – нет. Например:

11 – здесь первая единица обозначает десять, а вторая – 1.
II – здесь обе единицы обозначают единицу.

345, 259, 521 – здесь цифра 5 в первом случае обозначает 5, во втором – 50, а в третьем – 500.

XXV, XVI, VII – здесь, где бы ни стояла цифра V, она везде обозначает пять единиц. Другими словами, величина, обозначаемая знаком V, не зависит от его позиции.

Сложение, умножение и другие математические операции в позиционных системах счисления выполнить легче, чем в непозиционных, т.к. математические операции осуществляются по несложным алгоритмам (например, умножение в столбик, сравнение двух чисел).

В мире наиболее распространены позиционные системы счисления. Помимо знакомой всем с детства десятичной (где используется десять цифр от 0 до 9), в технике широкое распространение нашли такие системы счисление как двоичная (используются цифры 0 и 1), восьмеричная и шестнадцатеричная.

Следует отметить, важную роль нуля. «Открытие» этой цифры в истории человечества сыграло большую роль в формировании позиционных систем счисления.

Основание системы счисления – это количество знаков, которое используется для записи цифр.

Разряд - это позиция цифры в числе. Разрядность числа - количество цифр, из которых состоит число (например, 264 - трехразрядное число, 00010101 - восьмиразрядное число). Разряды нумеруются справа на лево (например, в числе 598 восьмерка занимает первый разряд, а пятерка - третий).

Итак, в позиционной системе счисления числа записываются таким образом, что каждый следующий (движение справа на лево) разряд больше другого на степень основания системы счисления. (придумать схему)

Одно и тоже число (значение) можно представить в различных системах счисления. Представление числа при этом различно, а значение остается неизменным.

Системой счисления называется совокупность приемов и правил для записи чисел цифровыми знаками. Любая предназначенная для практического применения система счисления должна обеспечивать:

· возможность представления любого числа в рассматриваемом диапазоне величин;

· единственность представления (каждой комбинации символов должна соответствовать одна и только одна величина);

· простоту оперирования числами.

Все системы представления чисел делят на позиционные и непозиционные.

Непозиционная система счисления – система, для которой значение символа не зависит от его положения в числе.

Для их образования используют в основном операции сложения и вычитания. Например, система с одним символом-палочкой встречалась у многих народов. Для изображения какого-то числа в этой системе нужно записать количество палочек, равное данному числу. Эта система неэффективна, так как запись числа получается длинной. Другим примером непозиционной системы счисления является римская система, использующая набор следующих символов: I, V, X, L, C, D, M и т. д. В этой системе существует отклонение от правила независимости значения цифры от положения в числе. В числах LX и XL символ X принимает два различных значения: +10 – в первом случае и –10 – во втором случае.

Позиционная система счисления – система, в которой значение символа определяется его положением в числе: один и тот же знак принимает различное значение. Например, в десятичном числе 222 первая цифра справа означает две единицы, соседняя с ней – два десятка, а левая – две сотни.

Любая позиционная система характеризуется основанием. Основание (базис) позиционной системы счисления – количество знаков или символов, используемых для изображения числа в данной системе.

Для позиционной системы счисления справедливо равенство

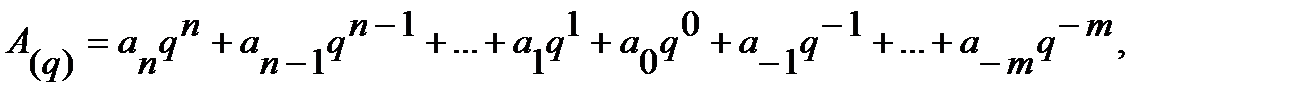
(1)

где A_(q) – произвольное число, записанное в системе счисления с основанием q; a_i – коэффициенты ряда (цифры системы счисления); n, m – количество целых и дробных разрядов.

На практике используют сокращенную запись чисел:

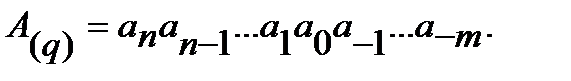(2)

Например:

а) в двоичной системе (q=2)

11010.101₂ = 1 · 2⁴ + 1 · 2³ + 0 · 2² + 1 · 2¹ + 0 · 2⁰ + 1 · 2^-1 + 0 · 2^-2 + 1 · 2^-3;

б) в троичной системе (q=3)

22120.212₃ = 2 · 3⁴ + 2 · 3³ + 1 · 3² + 2 · 3¹ + 0 · 3⁰ + 2 · 3^-1 + 1 · 3^-2 + 2 · 3^-3;

в) в шестнадцатиричной системе (q=16)

A3F.1CD₁₆ = A · 16² + 3 · 16¹ + F · 16⁰ + 1 · 16^-1 + C · 16^-2 + D · 16^-3.