Алфавитный подход к определению количества информации

Алфавитный подход используется для измерения количества информации в тексте, представленном в виде последовательности символов некоторого алфавита. Такой подход не связан с содержанием текста. Количество информации в этом случае называется информационным объемом текста, который пропорционален размеру текста — количеству символов, составляющих текст. Иногда данный подход к измерению информации называют объемным подходом.

Каждый символ текста несет определенное количество информации. Его называют информационным весом символа. Поэтому информационный объем текста равен сумме информационных весов всех символов, составляющих текст.

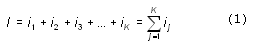
Здесь предполагается, что текст — это последовательная цепочка пронумерованных символов. В формуле (1) i₁обозначает информационный вес первого символа текста, i₂—информационный вес второго символа текста и т.д.; K —размер текста, т.е. полное число символов в тексте.

Все множество различных символов, используемых для записи текстов, называется алфавитом. Размер алфавита — целое число, которое называется мощностью алфавита. Следует иметь в виду, что в алфавит входят не только буквы определенного языка, но все другие символы, которые могут использоваться в тексте: цифры, знаки препинания, различные скобки, пробел и пр.

Определение информационных весов символов может происходить в двух приближениях:

1) в предположении равной вероятности (одинаковой частоты встречаемости) любого символа в тексте;

2) с учетом разной вероятности (разной частоты встречаемости) различных символов в тексте.

Приближение равной вероятности символов в тексте

Если допустить, что все символы алфавита в любом тексте появляются с одинаковой частотой, то информационный вес всех символов будет одинаковым. Пусть N — мощность алфавита. Тогда доля любого символа в тексте составляет 1/N-ю часть текста. По определению вероятности эта величина равна вероятности появления символа в каждой позиции текста:

p = 1/N

Согласно формуле К.Шеннона, количество информации, которое несет символ, вычисляется следующим образом:

i = log₂(1/p) = log₂N (бит)(2)

Следовательно, информационный вес символа (i) и мощность алфавита (N) связаны между собой по формуле Хартли 2ⁱ = N.

Зная информационный вес одного символа (i) и размер текста, выраженный количеством символов (K), можно вычислить информационный объем текста по формуле:

I = K · i (3)

Эта формула есть частный вариант формулы (1), в случае, когда все символы имеют одинаковый информационный вес.

Из формулы (2) следует, что при N = 2 (двоичный алфавит) информационный вес одного символа равен 1 биту.

С позиции алфавитного подхода к измерению информации 1 бит— это информационный вес символа из двоичного алфавита.

Более крупной единицей измерения информации является байт.

1 байт— это информационный вес символа из алфавита мощностью 256.

Поскольку 256 = 2⁸, то из формулы Хартли следует связь между битом и байтом:

2ⁱ = 256 = 2⁸

Отсюда: i = 8 бит = 1 байт

Для представления текстов, хранимых и обрабатываемых в компьютере, чаще всего используется алфавит мощностью 256 символов. Следовательно, 1 символ такого текста “весит” 1 байт.

Приближение разной вероятности встречаемости символов в тексте

В этом приближении учитывается, что в реальном тексте разные символы встречаются с разной частотой. Отсюда следует, что вероятности появления разных символов в определенной позиции текста различны и, следовательно, различаются их информационные веса.

Статистический анализ русских текстов показывает, что частота появления буквы “о” составляет 0,09. Это значит, что на каждые 100 символов буква “о” в среднем встречается 9 раз. Это же число обозначает вероятность появления буквы “о” в определенной позиции текста: p_o = 0,09.Отсюда следует, что информационный вес буквы “о” в русском тексте равен:

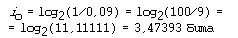
Самой редкой в текстах буквой является буква “ф”. Ее частота равна 0,002. Отсюда:

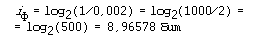
Отсюда следует качественный вывод: информационный вес редких букв больше, чем вес часто встречающихся букв.

Как же вычислить информационный объем текста с учетом разных информационных весов символов алфавита? Делается это по следующей формуле:

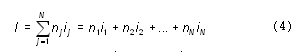
Здесь N — размер (мощность) алфавита; n_j — число повторений символа номер j в тексте; i_j — информационный вес символа номер j.

Таким образом, Алфавит — упорядоченный набор символов, используемый для кодирования сообщений на некотором языке. Мощность алфавита — количество символов алфавита.

Двоичный алфавит содержит 2 символа, его мощность равна двум.

Сообщения, записанные с помощью символов ASCII, используют алфавит из 256 символов. Сообщения, записанные по системе UNICODE, используют алфавит из 65 536 символов.

Чтобы определить объем информации в сообщении при алфавитном подходе, нужно последовательно решить задачи:

Определить количество информации (i) в одном символе по формуле 2ⁱ = N, где N — мощность алфавита

Определить количество символов в сообщении (m)

Вычислить объем информации по формуле: I = i * K.

Количество информации во всем тексте (I), состоящем из K символов, равно произведению информационного веса символа на К:

I = i * К.