Цифровое моделирование.

Цифровое моделирование на современном этапе развивается наиболее динамично. Это связано с интенсивным развитием математического обеспечения, формирующегося в виде пакетов прикладных программ. Использование этих пакетов повышает производительность моделирования и одновременно упрощает его.

Достоинства метода цифрового моделирования:

1. Решается любой класс задач подлежащих математической интерпретации;

2. Высокая точность решения (ограничена только временем решения задачи);

3. Легкость перехода от одной задачи к другой (необходимо лишь перезапустить программу);

4. Возможность исследования объектов высокой размерности.

Недостаток метода цифрового моделирования – конечное время моделирования, которое может не совпадать с реальным временем.

Цифровая вычислительная машина - это комплекс технических устройств, в которых могут протекать процессы, отображающие (моделирующие) действия с числами. Именно действия над числами составляют суть вычислительных операций при численном решении различных математических задач. Моделирование процесса численного решения математической задачи на ЦВМ практически означает автоматическое решение ее с помощью ЦВМ.

Числа могут не только выражать значение постоянных и переменных величин, но и являться символическими условными моделями самых разнообразных других объектов - букв, слов, предметов, явлений и т.д. Это позволяет свести к действиям над числами различные невычислительные задачи, например, определение числа объектов с заданными свойствами. Благодаря этому возможно моделирование на ЦВМ процедуры решения невычислительной задачи, т.е. машинная реализация этого решения.

Процесс функционирования любого материального объекта представляет последовательную смену его состояний во времени, каждое из которых определяют конкретные значения некоторых физических величин. Если объект является непрерывной системой, то эти величины - непрерывные функции непрерывного времени.

Математическое описание объекта составляют различные математические формы выражения количественных соотношений между переменными и постоянными. Это различные функции, уравнения, системы уравнений, условия однозначности их решений, неравенства и другие математические представления.

Если известно математическое описание функционирования объекта-оригинала, согласно этому описанию определен процесс над числами, выражающими значения величин, характеризующих состояние объекта, и этот процесс отображен в ЦВМ, то процесс, реализуемый ЦВМ, является материальной функциональной формальной математической подобной цифровой моделью оригинала.

Дискретная природа функционирования ЦВМ требует, как правило, приведение исходного математического описания оригинала к виду, удобному для цифрового моделирования. Прежде всего необходима дискретизация непрерывных величин. При этом непрерывные функции подвергаются квантованию по уровню и аргументу. В результате непрерывная функция непрерывного аргумента y = f( t ) превращается в дискретную функцию дискретного аргумента

T_yk_y = f ( Tk ),

где k и k_y - числа принимающие значения 0, ± 1, ± 2, ± 3, ... ; T и Ty - кванты переменных t и y.

Квантование по уровню - это замена значения y соответствующим числом определенной разрядности, сопровождающаяся погрешностью округления

D_y < T_y/2.

Поскольку в современных ЦВМ число разрядов велико 32 и более и погрешность пренебрежимо мала, поэтому практически можно считать, что функционирование ЦВМ описывается решетчатыми функциями вида

y = f ( Tk ) = f [ k ]

и моделирует их.

Для цифрового моделирование оригинала необходима алгоритмизация математического описания оригинала. Алгоритм - это точно определенное правило выполнения расчетных операций над числами, последовательность которых составляет общий процесс преобразования исходных данных в результат решения соответствующей задачи. Алгоритмизация математического описания заключается в получении соответствующего этому описанию алгоритма. Если, например, функционирование оригинала описывается дифференциальным уравнением, то алгоритмизация заключается в составлении алгоритма численного решения этого уравнения. По существу алгоритмизация математического описания и заключается в приведении его к виду, удобному для цифрового моделирования. Она выполняется на основе выбранного численного метода решения задачи, который позволяет свести решение к арифметическим действиям. При этом часто оказывается полезным применение аппарата решетчатых функций

Алгоритм может быть представлен в трех основных формах: аналитической, словесной и структурной.

Аналитическая форма алгоритма - это выражение его в виде явной функции соответствующих аргументов или в виде рекуррентной формулы. Форма отличается большой компактностью, но возможности применения ее ограничены.

Словесная форма алгоритма - это его описание его на естественном языке, обстоятельная инструкция для лица, решающего задачу вручную на бумаге. Форма является универсальной, но отличается громоздкостью и отсутствием наглядности.

Структурная форма алгоритма - это его описание в виде структурной схемы, состоящей из отдельных блоков, соединенных прямыми линиями. Каждый блок соответствует некоторой операцией над числами. Форма является универсальной, компактной и наглядной. Поэтому она используется наиболее часто.

В целом процесс моделирования на ЦВМ состоит из следующих этапов:

1. Составление исходного алгоритма, т.е. алгоритмизация математического описания оригинала.

2. Составление промежуточного алгоритма на алгоритмическом языке.

3. Получение машинного алгоритма.

4. Отладка программы.

5. Машинная реализация решения задачи.

Первые четыре подготовительных этапа значительно упрощаются благодаря применению типовых алгоритмов и соответствующих им стандартных программ, заранее составленных и многократно используемых для решения таких задач, как вычисление элементарных функций, определение нулей полиномов, перевод чисел из одной системы счисления в другую и др.

Комплекс программных средств, предназначенных для снижения трудоемкости подготовительной работы, повышения эффективности использования машины и облегчения ее эксплуатации, называется математическим обеспечением ЦВМ.

При цифровом моделировании наиболее часто приходится иметь дело с решетчатыми функциями f[k], соответствующими непрерывным функциям непрерывного аргумента. Непрерывная функция, совпадающая с дискретами решетчатой функции, называется огибающей этой решетчатой функции. Каждая непрерывная функция f(t) может служить огибающей различных решетчатых функций f_i[k] = f(T_ik), отличающихся параметром T_i - периодом дискретизации функции f(t). Каждая решетчатая функция может иметь множество различных огибающих.

Различным математическим формам и представлениям, характеризующим или определяющим непрерывную функцию f(t), можно поставить в соответствие аналоги, характеризующие или определяющие решетчатую функцию f(k). Аналогом первой производной функции f(t)

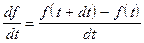
являются первое разностное уравнение функции f[k]

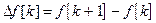, т.е. совершается переход к численным методам решения.

Итак, окончательно,

* первым этапом является при проектировании является выбор наиболее подходящей математической модели. Этот этап должен обеспечить получение наиболее удачной математической модели и выработке требований к условиям модели;

* вторым этапом процесса проектирования является подготовка математической модели для моделирования. Задача решается приведением к структурной схеме дискретного процесса и приведением системы уравнений к дискретной форме. Этот этап завершается двумя результатами: математическим описанием и структурной схемой всей дискретной системы. Структурная схема полученной дискретной системы должна быть идентична структурной схеме непрерывной системы по потоку информации;

* третьим этапом является написание программы для осуществления математического моделирования. Это решающий этап, содержащий строгое соблюдение временных соотношений в синтезируемой математической модели, как правило наибольшее число проблем возникает при переходе от задач 2го этапа к задачам 3го этапа;

*четвертый этап испытание, проверка и отладка модели, после которого получается законченная модель.