Структурирование при цифровом моделировании.
Как уже отмечалось, для успешного моделирования (особенно сложных систем) желательно в той или иной мере структурировать объект. Для этого объект разбивается на блоки.
Разумеется, можно использовать традиционный путь: используя структурную схему системы регулирования, свернуть её по правилам теории автоматического регулирования (ТАУ), получить общую передаточную функцию, а затем получить общее уравнение. Однако это не будет наглядной моделью отражающей физическую реальность.
Для сравнения выберем два варианта составления дифференциальных уравнений: по отдельным звеньям и по связи их в общую цифровую модель.
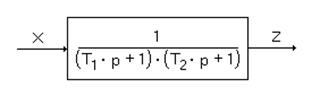
|
В качестве примера возьмём систему второго порядка состоящую из двух апериодических звеньев, которая можнт быть представлена в свёрнутом (рис. 37) и развёрнутом (рис. 38) виде.
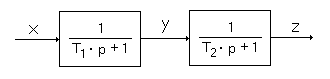
|
Рис. 55 Система регулирования в свёрнутом виде.
Рис. 56 Система регулирования в развёрнутом виде.
I. Выведем передаточную функцию системы представленной на рисунке 37:
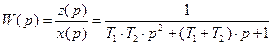 (79)
(79)
или
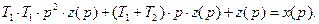 (80)
(80)
Известно, что уравнение высшего порядка может быть сведено к системе уравнений первого порядка.
Переход во временную область:
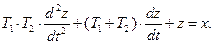 (81)
(81)
Введём вспомогательную переменную:
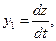 (82)
(82)
с учётом вспомогательной переменной перепишем уравнение (81)
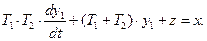 (83)
(83)
Таким образом, записав передаточную функцию и выполнив подстановку вспомогательной переменной, получим систему дифференциальных уравнений описывающих свернутую систему второго порядка:
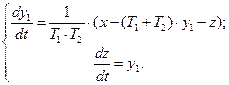 (84)
(84)
Аналогично можно составить систему уравнений для более высоких порядков.
Необходимо отметить, что замена переменной справедлива в том случае, если в числителе передаточной функции нет оператора 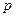 , его наличие вызывает осложнение при выводе общего уравнения.
, его наличие вызывает осложнение при выводе общего уравнения.
II. Запишем систему уравнений для развёрнутой системы представленной на рисунке 38.
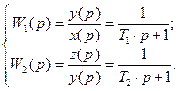 (85)
(85)
Используя передаточные функции (см. (85)) выведем математическое описание в операторной форме:
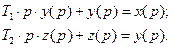 (86)
(86)
Переход во временную область для представления математического описания в форме дифференциальных уравнений:
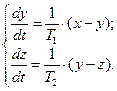 (87)
(87)
Математические описания (84) и (87) по форме эквивалентны. Для доказательства эквивалентности необходимо ввести в систему (87) промежуточную переменную 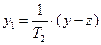 . После соответствующих преобразований система (87) будет полностью эквивалентна системе уравнений (84).
. После соответствующих преобразований система (87) будет полностью эквивалентна системе уравнений (84).
Составление уравнений по звеньям имеет преимущество, т.к. не требуется вводить вспомогательные переменные; и составление уравнений по звеньям имеет наглядность физических процессов протекающих в отдельных структурах.
Выбор вспомогательных переменных для передаточных функций, содержащих оператор 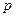 в числителе
в числителе
Оператор 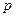 содержится в числителе таких передаточных функций, как форсирующие звенья. Передаточная функция форсирующего звена:
содержится в числителе таких передаточных функций, как форсирующие звенья. Передаточная функция форсирующего звена:
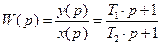 (88)
(88)
или
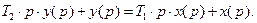 (89)
(89)
Во временной области:
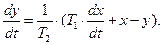 (90)
(90)
В принципе это уравнение применять нежелательно, т.к. в правой части содержится производная входного сигнала, которую необходимо вычислять численным методом, либо нужна функциональная зависимость входного сигнала от времени и тогда производную можно задать аналитически. К тому же такое уравнение обычными заменами переменных не сможем привести к форме Коши.
Уравнение (89) разделим на оператор 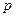 :
:
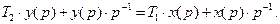 (91)
(91)
Введём замену переменных:
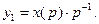 (92)
(92)
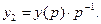 (93)
(93)
или
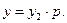 (94)
(94)
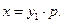 (95)
(95)
Выполнив замену переменных и осуществив переход во временную область, получим математическое описание форсирующего звена состоящую из двух дифференциальных и одного алгебраического уравнений:
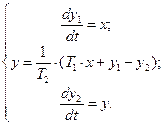 (96)
(96)
По функциям  и
и 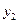 находят искомую функцию
находят искомую функцию 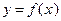 .
.
Как уже отмечалось, выбор промежуточных переменных позволяет получить различную форму записи дифференциальных уравнений.
Например, в методе переменных состояний используется следующий подход для вывода дифференциальных уравнений. Используем передаточную функцию (88), преобразуем её:
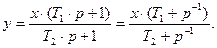 (97)
(97)
Введём вспомогательную функцию:
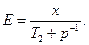 (98)
(98)
Следовательно,
 (99)
(99)
и
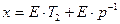 (100)
(100)
введём дополнительную вспомогательную переменную 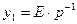 , получим:
, получим:
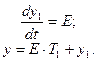 (101)
(101)
Выразим Е через х (см. выражение 100):
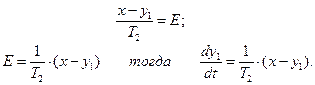 (102)
(102)
Окончательно система запишется в виде:
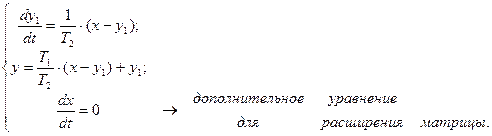 (103)
(103)
Дата добавления: 2015-11-10; просмотров: 712;
