Компьютерное моделирование. Принципы моделирования.

Традиционно под моделированием на ЭВМ понималось лишь имитационное моделирование. Можно, однако, увидеть, что и при других видах моделирования компьютер может быть весьма полезен. Например, при математическом моделировании выполнение одного из основных этапов — построение математических моделей по экспериментальным данным — в настоящее время просто немыслимо без компьютера. В последние годы, благодаря развитию графического интерфейса и графических пакетов, широкое развитие получило компьютерное структурно-функциональное моделирование, о котором подробно поговорим ниже. Положено начало привлечения компьютера даже к концептуальному моделированию, где он используется, например, при построении систем искусственного интеллекта.

Таким образом, мы видим, что понятие «компьютерное моделирование» значительно шире традиционного понятия «моделирование на ЭВМ» и нуждается в уточнении, учитывающем сегодняшние реалии.

Начнем с термина «компьютерная модель». В настоящее время под компьютерной моделью чаще всего понимают:

· условный образ объекта или некоторой системы объектов (или процессов), описанный с помощью взаимосвязанных компьютерных таблиц, блок-схем, диаграмм, графиков, рисунков, анимационных фрагментов, гипертекста и т. д. и отображающий структуру элементов объекта и взаимосвязи между ними. Компьютерные модели такого вида мы будем называть структурно-функциональными;

· программу или программный комплекс, позволяющий с помощью последовательности вычислений и графического отображения их результатов воспроизводить (имитировать) процессы функционирования объекта, системы объектов при условии воздействия на объект различных, как правило, случайных, факторов. Такие модели мы будем далее называть имитационными.

Компьютерное моделирование — метод решения задачи анализа или синтеза сложной системы на основе использования ее компьютерной модели. Суть компьютерного моделирования заключена в получении количественных и качественных результатов по имеющейся модели. Качественные выводы, получаемые по результатам анализа, позволяют обнаружить неизвестные ранее свойства сложной системы: ее структуру, динамику развития, устойчивость, целостность и др. Количественные выводы в основном носят характер прогноза некоторых будущих или объяснения прошлых значений переменных, характеризирующих систему.

Предметом компьютерного моделирования могут быть: экономическая деятельность фирмы или банка, промышленное предприятие, информационно-вычислительная сеть, технологический процесс, любой реальный объект или процесс, например процесс инфляции, и вообще – любая сложная система. Цели компьютерного моделирования могут быть различными, »однако наиболее часто моделирование является, как уже отмечалось ранее, центральной процедурой системного анализа, причем под системным анализом мы далее понимаем совокупность методологических средств, используемых для подготовки и принятия решений экономического, организационного, социального или технического характера.

Компьютерная модель сложной системы должна, по возможности, отображать все основные факторы и взаимосвязи, характеризующие реальные ситуации, критерии и ограничения. Модель должна быть достаточно универсальной, чтобы описывать близкие по назначению объекты, и в то же время достаточно простой, чтобы позволить выполнить необходимые исследования с разумными затратами.

Все это говорит о том, что моделирование систем, рассматриваемое в целом, представляет собой скорее искусство, чем сформировавшуюся науку с самостоятельным набором средств отображения явлений и процессов реального мира. Поэтому исключительно сложными, а по нашему мнению, и невозможными, являются попытки классификации задач компьютерного моделирования или создания достаточно универсальных инструментальных средств компьютерного моделирования произвольных объектов. Однако если преднамеренно сузить класс рассматриваемых объектов, ограничившись, например, задачами компьютерного моделирования при системном анализе объектов экономико-организационного управления, то возможно отобрать ряд достаточно универсальных подходов и программных средств.

Тема № 1.3 КОМПЬЮТЕРНОЕ МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ. ЭТАПЫ И ЦЕЛИ.

КОМПЬЮТЕРНОЕ МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ.

Математическая модель выражает существенные черты объекта или процесса языком уравнений и других математических средств. Собственно говоря, сама математика обязана своим существованием тому, что она пытается отразить, т. е. промоделировать на своем специфическом языке закономерности окружающего мира. Огромный толчок развитию математического моделирования дало появление ЭВМ, хотя сам метод зародился одновременно с математикой тысячи лет назад.

Математическое моделирование как таковое отнюдь не всегда требует компьютерной поддержки. Каждый специалист, профессионально занимающийся математическим моделированием, делает все возможное для аналитического исследования модели. Аналитические решения (т. е. представленные формулами, выражающими результаты исследования через исходные данные) обычно удобнее и информативнее численных. Однако, возможности аналитических методов решения сложных математических задач очень ограничены и, как правило, эти методы гораздо сложнее численных. В нашем курсе доминируют численные методы, реализуемые на компьютерах. Отметим, что понятия «аналитическое решение» и «компьютерное решение» отнюдь не противостоят друг другу, так как

а) все чаще компьютеры при математическом моделировании используются не только для численных расчетов, но и для аналитических преобразований;

б) результат аналитического исследования математической модели часто выражен столь сложной формулой, что при взгляде на нее не складывается наглядного восприятия описываемого ею процесса. Эту формулу (хорошо еще, если просто формулу!) нужно протабулировать, представить графически, проиллюстрировать в динамике, иногда даже озвучить, т.е. проделать то, что называется «визуализацией». Очевидно, возможности современных компьютеров наилучшим образом соответствуют этой задаче.

ЭТАПЫ И ЦЕЛИ КОМПЬЮТЕРНОГО МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

Рассмотрим процесс компьютерного математического моделирования, включающий численный эксперимент с моделью (рис. 1).

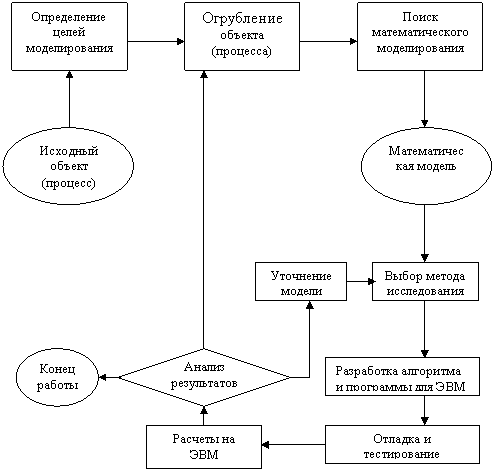
Рис.1. Общая схема процесса компьютерного математического моделирования

Первый этап – определение целей моделирования. Основные из них таковы:

1) Понимание

Модель в этой ситуации нужна для того, чтобы понять, как устроен конкретный объект, какова его структура, основные свойства, законы развития и взаимодействия с окружающим миром.

2) Управление

Модель нужна для того, чтобы научиться управлять объектом (или процессом) и определить наилучшие способы управления при заданных целях и критериях;

З) Прогнозирование

Модель используется для того, чтобы прогнозировать прямые и косвенные последствия воздействия на объект заданными способами.

Поясним это на примерах. Пусть объект исследования – взаимодействие потока жидкости или газа с телом, являющимся для этого потока препятствием. Опыт показывает, что сила сопротивления потоку со стороны тела растет с ростом скорости потока, но при некоторой достаточно высокой скорости эта сила скачком уменьшается с тем, чтобы с дальнейшим увеличением скорости снова возрасти. Что же произошло, обусловив уменьшение силы сопротивления? Математическое моделирование позволяет получить четкий ответ: в момент скачкообразного уменьшения сопротивления вихри, образующиеся в потоке жидкости или газа позади обтекаемого тела, начинают отрываться от него и уноситься потоком.

Пример совсем из другой области: мирно сосуществовавшие со стабильными численностями популяции двух видов особей, имеющих общую кормовую базу, «вдруг» начинают резко менять численность – и здесь математическое моделирование позволяет (с известной долей достоверности) установить причину явления, или, по крайней мере, опровергнуть определенную гипотезу о его причинах.

Выработка концепции управления объектом – другая возможная цель моделирования. Какой режим полета самолета выбрать для того, чтобы полет был вполне безопасным и экономически наиболее выгодным? Как составить график выполнения сотен видов работ на строительстве большого объекта, чтобы оно закончилось в максимально короткий срок? Множество таких проблем систематически возникает перед экономистами, конструкторами, учеными.

Наконец, прогнозирование последствий тех или иных воздействий на объект может быть как относительно простым делом (в несложных физических системах), так и чрезвычайно сложным – на грани выполнимости – в системах биолого-экономических, социальных. Если относительно легко ответить на вопрос об изменении режима распространения тепла в тонком стержне в зависимости от изменений в составляющем его сплаве, то несравненно труднее проследить (предсказать) экологические и климатические последствия строительства крупной ГЭС или социальные последствия изменений налогового законодательства. Возможно, и здесь методы математического моделирования будут оказывать в будущем более значительную помощь.

Составим список величин, от которых зависит поведение объекта или ход процесса, а также тех величин, которые желательно получить в результате моделирования. Обозначим первые из них (входные) через x₁, x₂,..., х_n,,; вторые (выходные) через y₁, y₂,…,y_n. Символически поведение объекта или процесса можно представить в виде

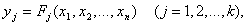
где F_j — те действия, которые следует произвести над входными параметрами, чтобы получить результаты. Хотя запись 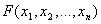напоминает обозначение функции, мы здесь используем ее в более широком смысле. Лишь в простейших ситуациях здесь F есть функция в обычном смысле; чаще всего она выражает лишь наличие некоторой связи между входными и выходными параметрами модели.

Входные параметры х_i могут быть известны «точно», т.е. поддаваться (по крайней мере, в принципе) измерению однозначно и с любой степенью точности — тогда они являются детерминированными величинами. Так, в классической механике, сколь сложной ни была бы моделируемая система, входные параметры детерминированы и, соответственно, детерминирован процесс эволюции такой системы. Однако в природе и обществе гораздо чаще встречаются процессы иного рода, когда значения входных параметров известны лишь с определенной степенью вероятности, т.е. эти параметры являются вероятностными (стохастическими), и, соответственно, случайным является процесс эволюции системы.

Случайный – не значит непредсказуемый. Просто в этой ситуации характер исследования и задаваемых вопросов резко меняется – они приобретают вид «С какой вероятностью...?», «С каким математическим ожиданием...?» и т.п. Примеров случайных процессов не счесть как в науке, так и в обыденной жизни (силы, действующие на летящий самолет в ветреную погоду; переход улицы при большом потоке транспорта и т.д.).

Для стохастической модели выходные параметры могут быть как величинами вероятностными, так и однозначно определяемыми. Например, на перекрестке улиц можно ожидать зеленого сигнала светофора и полминуты, и две минуты (с разной вероятностью), но среднее время ожидания есть величина вполне определенная, и именно она может быть объектом моделирования.

Важнейшим этапом моделирования является разделение входных параметров по степени важности влияния их изменений на выходные. Такой процесс называется ранжированием (разделением по рангам). Чаще всего невозможно, да и не нужно учитывать все факторы, которые могут повлиять на значения интересующих нас величин у_j. От того, насколько умело выделены важнейшие факторы, зависит успех моделирования, быстрота и эффективность достижения цели. Выделить наиболее значимые факторы и отсеять менее важные может лишь специалист в той предметной области, к которой относится модель. Так, опытный учитель знает, что на успех контрольной работы влияет степень знания предмета и психологический настрой класса; однако, влияют и другие факторы — например, каким уроком по счету идет контрольная, какова в этот момент погода и т.д. — фактически проведено ранжирование.

Отбрасывание менее значимых факторов огрубляет объект моделирования и способствует пониманию его главных свойств и закономерностей. Умело ранжированная модель должна быть адекватна исходному объекту или процессу в отношении целей моделирования. Обычно определить, адекватна ли модель можно только в процессе экспериментов с ней, анализа результатов первоначального моделирования.

На рис. 2 проиллюстрированы две крайние ситуации: а) некоторый параметр х_i, очень сильно влияет на результирующую величину у_i; б) почти не влияет на нее. Ясно, что если все представляющие интерес величины у_i реагируют на х_i, так, как изображено на рис. 2б, то х_i, является параметром, который при первом подходе может быть из модели исключен. Если же хотя бы одна из величин у_i реагирует на изменение х_i, так, как изображено на рис. 2а, то х_i нельзя исключать из числа значимых параметров.

Следующий этап — поиск математического описания. На этом этапе необходимо перейти от абстрактной формулировки модели к формулировке, имеющей конкретное

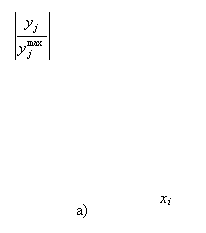
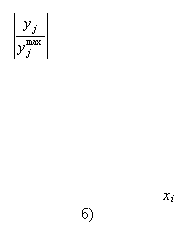
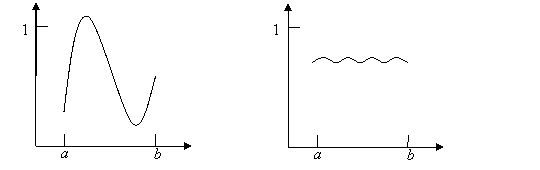
Рис. 7.2. Варианты степени влияния величины х_i на результирующую величину у_j

математическое наполнение. В этот момент модель предстает перед нами в виде уравнения, системы уравнений, системы неравенств, дифференциального уравнения или системы таких уравнений и т.д.

Когда математическая модель сформулирована, нужно выбрать метод ее исследования. Как правило, для решения одной и той же задачи есть несколько конкретных методов, различающихся эффективностью, устойчивостью и т.д. От верного выбора метода часто зависит успех всего процесса.

После разработки алгоритма и составления программы для ЭВМ необходимо решить с ее помощью простейшую тестовую задачу (желательно, с заранее известным ответом) с целью устранения грубых ошибок. Это лишь начало процедуры тестирования, которую трудно описать формально исчерпывающим образом. По существу, тестирование может продолжаться долго и закончиться тогда, когда пользователь по своим профессиональным признакам сочтет программу верной.

Затем следует собственно численный эксперимент, и выясняется, соответствует ли модель реальному объекту (процессу). Модель адекватна реальному процессу, если некоторые характеристики процесса, полученные на ЭВМ, совпадают с экспериментальными с заданной степенью точности. В случае несоответствия модели реальному процессу возвращаются к одному из предыдущих этапов.

1. Понятия моделирование, модель. Виды моделирования. Моделирование на ЭВМ.

Понятия компьютерное моделирование, компьютерная модель, функции

компьютера при моделировании.

2. Принципы моделирования. Общая классификация моделей. Требования к модели.

Виды математических моделей. Жизненный цикл моделируемой системы.

Операции над моделями.

3. Вычислительный эксперимент. Этапы вычислительного эксперимента.

Математическое и программное обеспечение эксперимента. Цикличность

эксперимента.

4. Линейность и нелинейность решаемых задач. Области применения

вычислительного эксперимента.

5. Понятие искусственный интеллект. Философские аспекты. Вопросы реализации.

Экспертные системы.

6. Программное обеспечение используемое в моделировании. Математические

пакеты. MathCad. Классы решаемых задач. Виды операции, типы переменных и

констант.