КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Компьютерные программы, как правило, относящиеся к стандартному программному обеспечению, осуществляют приближенное решение дифференциальных уравнений различными численными методами. Такое решение называют численным интегрированием. Численному интегрированию иногда может предшествовать приближенное, грубое графическое решение для осмысления дальнейших, более точных результатов. Прежде всего, непрерывное уравнение дискретизируется в соответствии с дискретным характером работы компьютера.
При численном интегрировании дифференциального уравнения (в общем случае нелинейного) первого порядка:
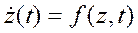
с начальным условием z(t0 ) = z0 выберем фиксированное приращение Δt=h независимой переменной t:
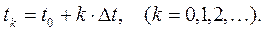
Вычисленные (приближенные) значения решения
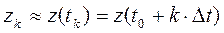
и производной
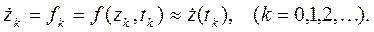
В том случае, если z(t ) представляет собой вектор, а f(z,t) – вектор-функцию правой части дифференциального уравнения, описывающего систему, то модель представляет собой систему уравнений (подобную тем, которые рассмотрены, например, для линейного случая в переменных состояния). Рекуррентные формулы любого из рассматриваемых ниже методов применяются к каждому из уравнений этой системы.
Дата добавления: 2015-09-18; просмотров: 989;
