Метод Эйлера. Метод Эйлерасостоит в пошаговом применении простой формулы, которая называется рекуррентной:
Метод Эйлерасостоит в пошаговом применении простой формулы, которая называется рекуррентной:
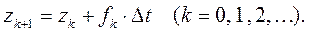 (3.1)
(3.1)
Метод Эйлерадает хорошее приближение решения только при достаточно малом шаге Δt = h и только для нескольких первых точек. Модификации этого метода определяются формулами:
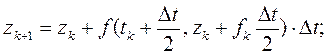 (3.2)
(3.2)
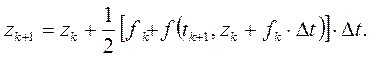 (3.3)
(3.3)
Эти модификации позволяют повысить точность интегрирования за счет «деления шага пополам».
3.3. Методы Рунге–Кутта
Методы Рунге–Куттазадаются приведенными ниже рекуррентными формулами. Методы (3.4) и (3.5) называют методами третьего порядка, поскольку формулы для zk+1 являются точными при f(z,t)=1, t, t2, t3; для достаточное количество раз дифференцируемой функции f(z,t) локальная ошибка усечения имеет порядок O(Δt4) при Δt→0. По аналогичным соображениям метод (3.6) называют методом четвертого порядка.
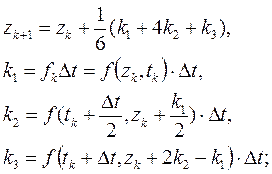 (3.4)
(3.4)
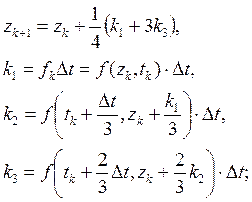 (3.5)
(3.5)
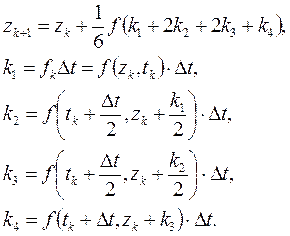 (3.6)
(3.6)
Из этих методов (3.6) является наиболее употребительным.
Дата добавления: 2015-09-18; просмотров: 1020;
