Контроль величины шага и устойчивость

Формулы интегрирования, выбранные из-за малой локальной ошибки усечения, могут способствовать накоплению ошибок в последовательности значений решения.

Выбор метода решения дифференциального уравнения требует некоторого компромисса между учетом локальной ошибки усечения, устойчивостью и временем расчета. Предпочтительнее те формулы, в которых слагаемые имеют одинаковые знаки и не слишком отличаются по абсолютной величине, так как при этом уменьшается влияние ошибок, вызванных округлением.

Окончательный выбор зависит от области применения и от применяемых вычислительных средств. Часто применяется двойная точность вычисления значений переменных.

Если данная функция f(z,t) очень сложная, то основное время расчета связано с вычислением ее значений. Для задачи Коши с умеренно гладкой функцией f(z,t) многошаговые схемы интегрированиятребуют относительно мало вычислений производных и допускают экономный автоматический контроль величины шага по величине .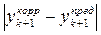

Методы Рунге–Куттаочень устойчивы и не требуют отдельной программы для начала решения. Они предпочтительнее для задач, связанных с частым изменением шага. Однако методы Рунге–Кутта требуют относительно большого количества вычислений производных на каждом шаге и для них весьма сложен эффективный контроль величины шага.

Вопросы к главе 3

1. Что называется численным интегрированием?
2. Что называется ошибкой усечения?
3. Чем отличается полная ошибка усечения от локальной?
4. Как получить рекуррентную формулу метода Эйлера из исходного непрерывного дифференциального уравнения?
5. От чего зависит порядок метода численного интегрирования?
6. Какими параметрами характеризуются методы численного решения дифференциальных уравнений?
7. В чем состоят преимущества и в чем недостатки метода Эйлера?
8. В чем состоят преимущества и в чем недостатки методов Рунге-Кутта?